Joker62 a écrit:Attention à la rédaction malgré tout.
La double flèche qui représente l'équivalence permet de passer d'une proposition à une autre équivalente.
Cela signifie que résoudre tel problème revient à résoudre tel problème.
Par exemple x^2 = 1 x^2 - 1 = 0
Toi tu finis par 48 ...
Ce qui ne veut rien dire... 48 n'est pas une proposition et n'a pas de valeur de vérité. 48 = 48 et c'est tout.
Pour la rédaction, on te demande de montrer qu'une expression est égale à une autre.
Il faut donc partir de l'expression de gauche, faire des manipulations et arriver à celle de droite.
Par exemple. On suppose que x = 1. Montrer que x+2 = 3.
On ne rédige pas ça sous la forme :
x + 2 = 3 x = 3-2 x = 1
Mais plutôt : x+2 = 1+2 (car x = 1) donc x+2 = 3. D'où x+2 = 3.
D'accord Joker62, donc j'ai rerédiger tout l'exercice et je pense que soit doit être mieux au niveau de la rédaction :
On sait d'après l'énoncé que

et

, d'où

et

Je sais aussi que si ces deux vecteurs sont orthogonaux, on a
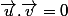
. Donc, on a :
^2-(\vec{u}+3\vec{v})^2=-32)
=-32)


On constate que :
^2-(\vec{u}+3\vec{v})^2=-8\vec{u}.\vec{v}-8\vec{v}^2)
^2-(\vec{u}+3\vec{v})^2=-8*0-8*4)
^2-(\vec{u}+3\vec{v})^2=0-32)
^2-(\vec{u}+3\vec{v})^2=-32)
Sinon, l'exercice j'y ai passé toute l'après-midi et j'en ai juste eu marre parce que au bout d'une heure et demi de sollicitation du cerveau au maximum :mur: , j'ai même pas une étincelle. Voici l'exercice qui me pose tant problème :
ABCD est un rectangle, AB=6 et AD=4.
1. Exprimez

et
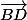
en fonction de

et

(Y a t-il un lien avec la projection orthogonale ? C'est la seule piste que j'ai pour l'instant..)
2. Déduisez-en que :

Merci de bien vouloir éclairer ma lanterne :id: , j'ai l'impression d'être nul

