Bonjour à tous,
J'ai un problème sur un exo de prépa, mais qui je pense est de niveau 1e. N'ayant pas le cours, j'aimerais vraiment avoir un rappel sur les règles de bases...
Voilà l'exo:
On pose f m (x) = (x+m)/(x²+1) et Cm sa courbe représentative.
Montrez que les tangentes aux courbes Cm au point d'abscisse 1 sont courantes.
Ce que j'ai fais:
Calcul de f'(x) = -x² -2mx + 1 / ((x²+1)²
f m (1) = m+1 / 2
f'(1) = - 1/2 m
y = (x-1)f'm(1) + f m (1) = -m/2(x-1) + (m+1)/2
Et là je bloque !! C'est à ça que se limitent mes connaissances sur les tangentes...
Merci d'avance pour votre aide.
P.S: Petite question à part. Est ce que quand une fonction est défini ainsi:
f: R+ --> R+ , cela signifie que non seulement x>0, mais f(x) > 0 également??
Problème tangente
13 messages
- Page 1 sur 1
Re: Problème tangente
Pour l'exo, je ne sais pas mais pour le PS je suis formel une fonction  ne peut retourner autre chose qu'un élément strictement positif
ne peut retourner autre chose qu'un élément strictement positif 
Re: Problème tangente
Pour être exacte: " De R+ dans R+" C'est pareil?
Je m'en doutais mais ça me semblait trop beau pour être vrai
Je m'en doutais mais ça me semblait trop beau pour être vrai
Re: Problème tangente
Abilys38 a écrit:f: R+ --> R+ , cela signifie que non seulement x>0, mais f(x) > 0 également??
Re: Problème tangente
L'équation de la tangente que tu a trouvé est 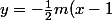+\frac{1}{2}(m+1)\Leftrightarrow m(x-2)+2y-1=0)
Donc toutes ces tangentes passent par le même point=(2,\frac{1}{2}))
CQFD
Donc toutes ces tangentes passent par le même point
CQFD
Re: Problème tangente
Merci pour ta réponse.
Quelque chose me dépasse avec ca. Je comprend le raisonnement que tu me montres. Mais, les équations selon chaque point de la courbe sont différentes, non? Ainsi, comment peut on dire à partir de CETTE équation, que les droites sont concourantes? (Pardon pour la faute dans l'énoncé, autocorrection iPad).
Quelque chose me dépasse avec ca. Je comprend le raisonnement que tu me montres. Mais, les équations selon chaque point de la courbe sont différentes, non? Ainsi, comment peut on dire à partir de CETTE équation, que les droites sont concourantes? (Pardon pour la faute dans l'énoncé, autocorrection iPad).
Re: Problème tangente
Montrez que les tangentes aux courbes Cm au point d'abscisse 1 sont courantes.
Ce sont les tangentes à
Donc on cherche un point par lequel passent toutes ces tangentes (tangentes au point d'abscisse 1). Il faut réordonner ton équation de la famille des tangentes (droites ayant pour paramètre
Re: Problème tangente
salut
deux remarques ::
1/ ne pas oublier que 0 est positif (d'ailleurs il est négatif aussi et c'est pourquoi il est nul !!) donc R+ désigne l'intervalle [0, +oo[
2/ Abilys38 :: il serait bien de connaître l'existence des parenthèses et savoir s'en servir quand elle sont nécessaires !!!
en bonus : avec geogebra et en créant un curseur m si tu traces les courbes des fonctions f_m et leur tangente au point d'abscisse 1 tu verras la réponse ...
deux remarques ::
1/ ne pas oublier que 0 est positif (d'ailleurs il est négatif aussi et c'est pourquoi il est nul !!) donc R+ désigne l'intervalle [0, +oo[
2/ Abilys38 :: il serait bien de connaître l'existence des parenthèses et savoir s'en servir quand elle sont nécessaires !!!
en bonus : avec geogebra et en créant un curseur m si tu traces les courbes des fonctions f_m et leur tangente au point d'abscisse 1 tu verras la réponse ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Problème tangente
Ok merci pour les explications. C'est la première fois que je fais un exercice avec un paramètre en plus (m), et je n'avais pas pensé à ça. Merci !!
Zygomatique, pourquoi cette remarque sur les parenthèses? A quoi fais tu référence?
Bonne journée !!
Zygomatique, pourquoi cette remarque sur les parenthèses? A quoi fais tu référence?
Bonne journée !!
Re: Problème tangente
ben à tes calculs où il manque des parenthèses ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
