Bonjour, j'ai des difficultés avec cet exercice sur les fonctions.Je ne comprends pas comment procéder pour répondre à la première question. J'ai essayé de remplacer y par 1m65, qui est la distance entre le ballon et le sol mais je ne pense pas que ce soit la bonne solution.
Merci par avance pour vos réponses.
Énoncé: Lors d'un lancer franc au basket, le joueur se situe a environ 4,60m du centre du panier, lui même fixé a 3,05m du sol.
Le joueur lance le ballon au niveau des épaules, c'est à dire à 1,65m du sol. On admettra que, dans le repère choisi, la courbe décrite dans l'espace par le ballon est la parabole déquation y=-0,5x²+1,95x+1,65, où x est la distance horizontale, en m, du ballon au joueur et y la hauteur, en m, du ballon au sol.
1) Peut-on affirmer que le joueur a réussi son panier ?
2) Quelle est la hauteur maximale atteinte par le ballon ?
Problème ouvert sur les fonctions
13 messages
- Page 1 sur 1
Salut,
1)
L'équation permet de déterminer la position de la balle à un moment donné du lancé. Plus précisément de déterminer sa hauteur lorsqu'on connait sa position horizontale. Ainsi on peut connaitre la hauteur de la balle lorsque celle-ci se trouve au niveau du panier, c'est-à-dire quand x = 4,60m car x représente la distance horizontale entre le ballon et le joueur et on sait que la distance entre le panier et le joueur est 4,60m.
y = f(4,60) est la hauteur de la balle lorsque la balle est à 4,60 mètres du joueur donc au niveau du panier. La balle est-elle à la hauteur du panier...?
2)
Pour trouver la hauteur maximale du ballon on peut directement utiliser la formule donnant l'abscisse du sommet d'une parabole de type
ax² + bx + c
On remarque que a = -0,5 < 0 donc la parabole est retournée (grosso modo la forme d'un U retourné) ainsi le sommet correspond bien au point le plus haut.
Formule qui est : x_sommet = -b/2a
x_sommet est la distance horizontale entre le joueur et la balle lorsque la balle est au plus haut. On peut retrouver la hauteur correspondante en calculant f(x_sommet)
1)
L'équation permet de déterminer la position de la balle à un moment donné du lancé. Plus précisément de déterminer sa hauteur lorsqu'on connait sa position horizontale. Ainsi on peut connaitre la hauteur de la balle lorsque celle-ci se trouve au niveau du panier, c'est-à-dire quand x = 4,60m car x représente la distance horizontale entre le ballon et le joueur et on sait que la distance entre le panier et le joueur est 4,60m.
y = f(4,60) est la hauteur de la balle lorsque la balle est à 4,60 mètres du joueur donc au niveau du panier. La balle est-elle à la hauteur du panier...?
2)
Pour trouver la hauteur maximale du ballon on peut directement utiliser la formule donnant l'abscisse du sommet d'une parabole de type
ax² + bx + c
On remarque que a = -0,5 < 0 donc la parabole est retournée (grosso modo la forme d'un U retourné) ainsi le sommet correspond bien au point le plus haut.
Formule qui est : x_sommet = -b/2a
x_sommet est la distance horizontale entre le joueur et la balle lorsque la balle est au plus haut. On peut retrouver la hauteur correspondante en calculant f(x_sommet)
Bonjour,
Je vais essayer de répondre même si ton énoncé me gêne un peu...
Le repère.
Je présume que l'axe des abscisses est porté par le plancher et que l'axe des ordonnées est porté par la verticale passant par le joueur ?
Dans ce cas
- les coordonnées du ballon au départ du tir sont (0;1,65)
- les coordonnées du centre du panier sont (4,6;3,05)
- le joueur tire et son ballon décrit la courbe d'équation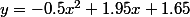
Si ces supputations sont exactes, alors si le point de coordonnées (4,6;3,05) est sur la courbe alors le panier est réussi, dans le cas contraire, non.
Q2 la hauteur maximale atteint par le ballon.
La méthode va dépendre de ton niveau et de ce que tu as appris.
Par exemple : l'abscisse du sommet de la parabole d'équation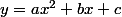 est
est 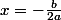 . As-tu vu cette formule ?
. As-tu vu cette formule ?
Sinon, saurais-tu écrire l'équation de la parabole décrite par le ballon sous la forme^2+y_S) ?
?
Bye
Je vois que je suis trop bavard et trop lent au clavier...
Je vais essayer de répondre même si ton énoncé me gêne un peu...
Le repère.
Je présume que l'axe des abscisses est porté par le plancher et que l'axe des ordonnées est porté par la verticale passant par le joueur ?
Dans ce cas
- les coordonnées du ballon au départ du tir sont (0;1,65)
- les coordonnées du centre du panier sont (4,6;3,05)
- le joueur tire et son ballon décrit la courbe d'équation
Si ces supputations sont exactes, alors si le point de coordonnées (4,6;3,05) est sur la courbe alors le panier est réussi, dans le cas contraire, non.
Q2 la hauteur maximale atteint par le ballon.
La méthode va dépendre de ton niveau et de ce que tu as appris.
Par exemple : l'abscisse du sommet de la parabole d'équation
Sinon, saurais-tu écrire l'équation de la parabole décrite par le ballon sous la forme
Bye
Je vois que je suis trop bavard et trop lent au clavier...
Ah oui je commence à comprendre.Merci pour votre aide.Donc pour la question 1 j'ai remplacé x et y par leurs équivalents, c'est à dire 4,60 et 3,05 pour résoudre l'équation mais je trouve comme résultat 3,05=53,4. Ça ne me semble pas logique. Dans mon énoncé, il est écrit que x est la distance du ballon au joueur (et non du joueur au panier). L'erreur est surement là ?
x est la distance du ballon au joueur (et non du joueur au panier)
Bin justement j'ai beaucoup réfléchi à cela et cette formulation m'avait paru étrange.
J'ai donc supposé que les pieds du joueur étaient l'origine des coordonnées, le sol l'axe des x, et le joueur l'axe des y.
Moyennant quoi x, distance du ballon au joueur, est l'abscisse du ballon dans le repère choisi.
Lorsque cette abscisse est de 4,6, le ballon se trouvant à 4,6 m du joueur est situé sur la verticale passant par le panier (abscisse du panier 4,6).
A cet instant, soit l'ordonnée du ballon sur la parabole est 3,05 et le panier est réussi, soit ce n'est pas le cas et le panier est raté...
Autrement dit avec
loy a écrit:Ah oui effectivement, c'est plus logique comme ça. Mais après avoir résolu mon équation f(4,6)=0.5 X 4,6²+1,95 X 4.6² + 1,65, je trouve comme résultat f(4,6)=32,2. Le résultat est ici très différent de 3,05. Est-ce normal ?
Hmmmmm...
Tu as oublié le - devant 0,5...
Pour x =4,6 , le ballon est environ à 4 cm du sol, le panier, lui est à 3,05 m.
La question est : panier réussi ou pas ?
Un bon réflexe : tracer la courbe avec ta calculette ou un grapheur sur un ordi.. (si on n'oublie pas de signe)
Bonjour,
=-0.5x^2+1.95x+1.64) c'est l'expression de la fonction f.
c'est l'expression de la fonction f.
Cette fonction a une courbe représentative d'équation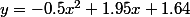 .
.
(0;1.65) sont les coordonnées du point de départ du ballon...
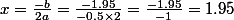 est l'abscisse du sommet de la parabole.
est l'abscisse du sommet de la parabole.
f(1,95) est l'ordonnée du sommet de cette parabole : f(1.95)=3.54125
Donc le ballon monte durant 1,95 m atteint une hauteur de 3,54125 m puis redescend....
Bye
Cette fonction a une courbe représentative d'équation
(0;1.65) sont les coordonnées du point de départ du ballon...
f(1,95) est l'ordonnée du sommet de cette parabole : f(1.95)=3.54125
Donc le ballon monte durant 1,95 m atteint une hauteur de 3,54125 m puis redescend....
Bye
seyrane35 a écrit:je ne comprend pas pourquoi vous utiliser des "y" alors qu'il n'y en a pas et que doit-on faire avec (1,95) ?
Lorsqu'on parle de fonction f(x) on parle implicitement de points placés sur un repère en 2 dimensions, les points de cette fonction sont donc repérés par 2 coordonnées, souvent noté x et y.
Lorsqu'on cherche un point situé sur la courbe, ayant sa coordonnée x (disons x = 1) on peut trouver sa coordonnée y qui est égale à f(1). Le point (1, f(1)) est sur la courbe, ça revient à la définition qui est de dire que tous les points sont repérables par les coordonnées (x, f(x))
Ici y donne la hauteur du ballon à un moment donné. x donne la distance entre le joueur et le ballon. On peut ainsi comme ça relier la hauteur et la distance x grâce à l'équation y = f(x) avec f(x) = l'expression dans l'énoncé.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
