Problème d'optimisation : plan, droite

[dazouzi]

Bonjour,

Tout d'abord, je vais vous donner les ingrédients du problème :
- Je travaille dans l'espace
- Dans cet espace, j'ai 3 points A, B, C (distincs)
- Les deux premiers points(A et B) définissent une droite. Au milieu de cette droite, nous allons créer un point M.
- Le dernier point(C) permet de définir un plan(P) comprenant la droite AB et le point C

Ce que je désire :
Déterminer la coordonnée du point D compris dans le plan P, tel que la droite MD soit perpendiculaire à AB.

Mes pistes :
Le problème est déjà résolu, cependant il n'est pas optimisé, c'est-à-dire que je n'arrive pas à trouver une solution plus rapide.
Voici ma démarche : Je crée le plan comprenant A, B et C
Je cherche les droites tel que celles-ci soit comprises dans ce plan et soient orthogonale à AB.
Je cherche la droite qui comprend le point M.

Auriez-vous une démarche plus simple ?

Merci :)

[Dlzlogic]

Bonjour,
Tout d'abord je voudrais savoir dans quel contexte exacte vous êtes
1- scolaire ou professionnel ?
2- manuel ou informatique
3- vrai 3D ou 2.5D

Sinon, votre démarche me parait très correcte.

[dazouzi]

Bonjour,
Tout d'abord je voudrais savoir dans quel contexte exacte vous êtes
1- scolaire ou professionnel ?
2- manuel ou informatique
3- vrai 3D ou 2.5D

Sinon, votre démarche me parait très correcte.

1 : Privé.
2 : Informatique.
3 : 3D.

[Dlzlogic]

Pour ce type de problème, en l'occurrence, calcul et visualisation d'objet en perspective, je me suis fait quelques fonctions de traitement de vecteurs en 3D, de façon que les problèmes de base soient résolus un fois pour toute. Si vous êtres en C/C++, je peux vous les donner. Mais la préoccupation, à mon avis, n'est pas l'optimisation, mais la facilité d'utilisation. Les pièges à éviter, donc à étudier une fois pour toutes, sont les cas qui se résument par "division par 0" et ce qui peut être plus grave, division par un nombre très petit. C'est à dire les cas de parallélisme non prévus.

[dazouzi]

Pour ce type de problème, en l'occurrence, calcul et visualisation d'objet en perspective, je me suis fait quelques fonctions de traitement de vecteurs en 3D, de façon que les problèmes de base soient résolus un fois pour toute. Si vous êtres en C/C++, je peux vous les donner. Mais la préoccupation, à mon avis, n'est pas l'optimisation, mais la facilité d'utilisation. Les pièges à éviter, donc à étudier une fois pour toutes, sont les cas qui se résument par "division par 0" et ce qui peut être plus grave, division par un nombre très petit. C'est à dire les cas de parallélisme non prévus.

Je suis intéressé par vos sources, peut-être y trouverais-je une solution.
J'ai déjà un moteur 3D, etc. Il s'agit ici d'un cas particulier qui demande que l’exécution soit plus rapide.

[chan79]

Bonjour,

. Au milieu de cette droite, nous allons créer un point M.


Merci

Salut
Tu pourrais préciser la définition de M ?

[Cliffe]

Déterminer la coordonnée du point D compris dans le plan P

Pour moi il y a une infinité de points.

J'ai fait ça. J'ai pas vérifier, à voir.

[dazouzi]

@chan79 : Je ne comprends pas ta question. Tu veux une définition formelle ?

@Cliffe : Oui, j'ai effectué la même démarche, elle est correcte mais pas très rapide.

Pour moi il y a une infinité de points.

Oui, il y a une infinité de points qui existe sur la droite. J'en demande juste la forme.

[Mortelune]

Je pense que chan79 veut dire qu'une droite n'a pas de milieu et qu'il aurait fallu lire M milieu du segment ...

Donc en fait on cherche une équation de l'intersection entre le plan médiateur P du segment AB (il passe par le milieu (M) de AB et est orthogonal à la droite AB) et le plan (ABC) ?

Et là je ne vois pas comment faire plus rapide que Cliffe, la définition d'une droite dans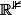 est l'intersection de deux plans, après, à partir du système on doit pouvoir trouver un vecteur directeur de la droite cherchée.

[dazouzi]

Oui, je suis toujours dessus.
Il y a, je pense, des démarches différentes qui demande moins de calculs, mais mes souvenirs me font défauts. Du style :
- On cherche la projection orthogonale, le point M, de D sur AB. Il n'y a pas qu'1 seul point, mais on peut donner la forme de ce point.
- Ce point doit appartenir au plan ABC, en d'autres mots, il suffit de vérifier si les 4 points sont coplanaires. Et finir par résoudre les équations..
Mais bon, là c'est une idée que je viens de pondre :doh:

[Mortelune]

Pour le premier point il y a bien une formule dans R², par changement de repère il devrait y avoir moyen de s'y ramener directement mais le changement de repère risque d'être assez lourd. Alors que là les deux équations de plans sont obtenues simplement par calcul et permettent de trouver facilement le vecteur directeur de la droite :


Voici deux équations de plan, dans notre cas on suppose en plus qu'ils sont sécants.
Donc en multipliant (1) par e et (2) par a on trouve y en fonction de z en faisant e(1)-a(2). De la même manière en multipliant (1) par f et (2) par b on trouve x en fonction de z en faisant f(1)-b(2). Ainsi on a tout en fonction de z. et on a un point de la droite (M), et un vecteur directeur du coup on a la droite.

[Cliffe]

Oui, j'ai effectué la même démarche, elle est correcte mais pas très rapide.

Tu peut tjr demandé a maple de te factoriser au maximum le résultat. Si c'est bien programmé tu pourra difficilement faire plus rapide (essaye en ASSEMBLEUR).

[dazouzi]

J'ai trouvé une solution bien plus rapide, le passage aux coordonnées polaires en choisissant M comme origine du repère et en changeant l'angle puis en repassant à R3.

Merci pour vos différentes réponses.

[fatal_error]

slt,

Je cherche les droites tel que celles-ci soit comprises dans ce plan et soient orthogonale à AB.

Plus simple.
tu cherches le projeté orthogonal de C sur (AB) que j'appele H.

et donnent

et tu trouves

Donc tu déduis H.
et après tu écris

donc tu connais D
donc tu connais le vecteur .

[dazouzi]

@fatal_error : Merci pour ta réponse. En effet, elle simplifie un peu la quantité de calculs.

Néanmoins la dernière solution que j'ai proposé reste tout de même la plus rapide.
Cependant, j'ai un problème.. Normalement, je dois faire un changement de repère pour que le repère 2D soit le plan ABC. Mais ne sachant plus comment faire, j'ai opté pour prendre uniquement les deux coordonnées cartésiennes de A(soustraites à M), puis transformées en coordonnées polaires, puis additionnées à PI/2 et finalement retransformées en coordonnées cartésiennes.
En faisant ça, j'obtiens 1 point D qui n'est pas forcément sur le plan ABC.
Pourriez-vous m'expliquez comment faire pour faire ce changement de repère ? Car pour l'instant, pour palier à ce problème, je fais en sorte que ce point D fasse partie du plan ABC par une projection orthogonale.

[Mortelune]

En étant en 3 dimensions il faudrait plutôt voir ça comme des coordonnées cylindriques avec un axe orthogonal au plan ABC et passant par M. A vu de nez ça ne semble pas évident.

[fatal_error]

@ dazouzi, je doute que ta méthode soit plus efficiente, cela dit j'ai pas remplacé, mais bon, c'est pénible de se trimballer le calcul littéral..

Pour changer te ramener dans le plan (MBC), il te suffit de considérer le vecteur u colinéaire à (MB) normé de préférence, de prendre le vecteur MC, et d'enlever sa composante colinéaire à (MB) pour obtenir un vecteur v orthogonal à u
genre également à normer...

enfin la rotation R de centre M s'écrit telle que
X'=RX,
avec w = u vectoriel v
avec X un point du plan et pour rester dans le plan généré par

avec a = pi/2
et X=C
on trouve D image de C en fonction de u, et v, et donc les coordo de D dans notre repère d'origine.
D=xC*(-u) + yC*v +zC * w