Probleme de limites !
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 12 Sep 2006, 18:28
par Benco » 12 Sep 2006, 18:28
Voila je suis en TS et j'ai un devoir maison cependant, connaisant les réponses aux limites ci-dessous, je n'arrive pas a voir comment les trouver sans ma calculette.
Merci de votre aide.
1) f(x) = racine( x + racine (x) ) - racine (x) limite en + l'infini ?
2) f(x) = ( 2 - racine ( 3x-2) ) / ( racine (2x+5) - 3 ) limite en 2 ?
3) f(x) = x sin (2/x) limite en 0 et en + l'infini ?
4) f(x) = racine ( x²+x+1) + x limite en - l'infini ?
Voila :p
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 12 Sep 2006, 18:31
par fonfon » 12 Sep 2006, 18:31
Salut, deja pour les limites avec les racines as-tu essayé l'expression conjuguée?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 12 Sep 2006, 18:34
par fonfon » 12 Sep 2006, 18:34
Re, et pour la limit avec le sinus fais un changement de variable en posant :
X=2/x
A+
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 12 Sep 2006, 18:45
par Benco » 12 Sep 2006, 18:45
Bonjour, pour les racines j'ai essayé les qauntités conjugués et pour ce qui est de changement de variable je connais pas cette methode, nous sommes qu'au debut de l'annee de TS !
Mais merci pour votre aide.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 12 Sep 2006, 18:51
par fonfon » 12 Sep 2006, 18:51
Re,
tu y arrives avec l'expression conjuguée?
sinon pour le changement de variable à mon avis on peut y penser même si tu es au debut de ta terminale car je pense que tu as dû voir que:
}{x}}=1)
non?
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 13 Sep 2006, 12:28
par Benco » 13 Sep 2006, 12:28
Oui c'est bon j'ai reussi a faire la limite de avec le sinus en + l'infini :p
Celle qui me bloque le plus est la 4°
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 12:47
par fonfon » 13 Sep 2006, 12:47
Salut,
({\sqrt{x^2+x+1}-x)}}{\sqrt{x^2+x+1}-x}=\frac{x+1}{\sqrt{x^2(1+\frac{1}{x}+\frac{1}{x^2})}-x}=...)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2006, 13:26
par Flodelarab » 13 Sep 2006, 13:26
fonfon a écrit:Salut,
({\sqrt{x^2+x+1}-x)}}{\sqrt{x^2+x+1}-x}=\frac{x+1}{\sqrt{x^2(1+\frac{1}{x}+\frac{1}{x^2})}-x}=...)
Que c compliqué!!!
et si on factorisait par x tout simplement ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 13:30
par fonfon » 13 Sep 2006, 13:30
Si tu factorises directement par x tu n'auras pas la bonne limite
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 13 Sep 2006, 13:55
par Benco » 13 Sep 2006, 13:55
Je suis arrivé exactement là ou tu m'as dit mais je fais quoi apres ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 14:01
par fonfon » 13 Sep 2006, 14:01
Re,
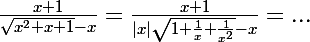
et en + inf ou -inf, la limite d'une fonction rationnelle est ...
ps:attention à la valeurs absolue)
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 13 Sep 2006, 15:18
par Benco » 13 Sep 2006, 15:18
Désolé je ne vois toujours pas car en plus dans ce dernier exemple vous passez de racine(..)-X a racine(..)+X ? Comment faites-vous ?
Merci deja pour votre precieuse aide :p
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 15:33
par fonfon » 13 Sep 2006, 15:33
oui, desolé c'est bien rac(..)-x
donc
}{|x|\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}-x})
or c'est la limite en -inf
donc
}{|x|\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}-x}=\frac{x(1+\frac{1}{x})}{-x(\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}+1)})
a toi de conclure
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2006, 16:20
par Flodelarab » 13 Sep 2006, 16:20
Comme qui dirait que je vois une factorisation par x ...
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 16:26
par fonfon » 13 Sep 2006, 16:26
je suis d'accord qu'il y a une factorisation par x mais si tu la fait au depart je pense qu'il va y avoir comme un problème
-
Benco
- Membre Naturel
- Messages: 56
- Enregistré le: 12 Sep 2006, 18:21
-
 par Benco » 13 Sep 2006, 17:03
par Benco » 13 Sep 2006, 17:03
La limite est donc -1/2 c'est ca ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 17:09
par fonfon » 13 Sep 2006, 17:09
c'est bien ça :++:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2006, 17:11
par Flodelarab » 13 Sep 2006, 17:11
fonfon a écrit:je suis d'accord qu'il y a une factorisation par x mais si tu la fait au depart je pense qu'il va y avoir comme un problème
ça risque pas!, on fait la meme !
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 17:18
par fonfon » 13 Sep 2006, 17:18
je sais pas car:
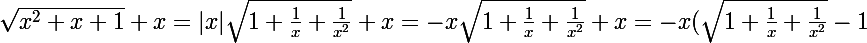)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2006, 17:40
par Flodelarab » 13 Sep 2006, 17:40
 = -x\frac{(\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}-1)(\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}+1)}{(\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}+1)} = -x\frac{\frac{1}{x}+\frac{1}{x^2}}{(\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}+1)} = ???)
Je refuse l'idée de la "bonne limite" ... qui a faux ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
