Un problème dèrière quelque chose d'anodin

par **Ben314** » 18 Déc 2009, 22:22

Tout à fait, mais en éliminant les cas où la différence entre les deux racines est plus grande que 1 (cas dans lesquels il y a forcément un entier dans l'intervalle), il ne te restera que "trés peu" de possibilités et donc que "trés peu" d'entier succeptibles de marcher.
En écrivant une inéquation pour chacun d'eux, tu devrait trouver le résultat.

P.S. j'ai pas fait les calculs...

par **benekire2** » 18 Déc 2009, 22:29

oui j'y réfléchis, je vais essayer de traduire ca ...

par **annick** » 18 Déc 2009, 23:35

Est-ce qu'un raisonnement simpliste de ce genre ne pourrait pas suffire ?

B(x)= -0.02x²+(p-20)x-40000
x>0
p>0

donc -0,02x²<0 et -40000<0

Pour que B(x) ne soit pas <0, il faut déjà au moins que (p-20)>0, soit p>20

par **Ben314** » 18 Déc 2009, 23:42

C'est "un peu juste" dans le sens que c'est une condition nécéssaire mais pas suffisante. Je pense que l'on ne peut pas s'en sortir sans utiliser le discriminant (ou la "forme canonique)

En plus, le fond du problème de bénékire, c'est qu'il veut totalement interpréter le coté "matériel" du problème, c'est à dire qu'il veut répondre à la question : "existe t'il un(des) entier(s) x tels que B(x) soit positifs" (dans son énoncé, x désigne le nombre de camion vendu et il considère que l'on ne vend pas des demi camions...)
Il a lui même dit que cette "subtilié" risquait d'avoir échapé à son prof. lorsqu'il leur à donné l'exo...

par **benekire2** » 19 Déc 2009, 07:18

C'est probable qu'il ait oublié .. ou non,
mais l'on a déjà vérifier un cas, celui des deux racines négatives, auquel j'ai conclu qu'il n'existe aucun p tel qu'il y ait deux racines négatives ...
Alors je me dit que mon prof a dû y réfléchir ( ou coup de chance ... quand même pas :zen: ) .
En revanche dans l'énoncé ou nous demande de déterminer p pour que le discriminant soit négatif , puis de conclure, mais ça m'a paru bizarre de considérer un raisonnement aussi simple.

par **benekire2** » 19 Déc 2009, 07:26

Finalement le dernier problème se ramène a essayer ddans un premier temps de trouver un écart entre les racines inférieur a 1 :

cela se rapporte a :

et j'ai pas le temps de résoudre, je part a Paris ...

par **Ben314** » 19 Déc 2009, 12:02

S'il y en a que le sujet interesse, je fait un petit rappel d'où on en est :
Enoncé :
On veut savoir pour quelles valeurs de p positif l'équation ax²+bx+c>0 (avec a=-0.02, b=p-20, c=-40000) admet une (des) solution(s) x entier naturel.
Réponse :

=b²-4ac=(p-20)²-3200
Donc, si

et de somme

(car p>20) donc les deux racines sont strictement positive.
L'ensemble des solutions réelles de l'inéquation est l'intervalle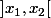

(contenu dans

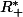) de largeur

(rappel : a1\ \Leftrightarrow\ \sqrt{\Delta}>-a\ \Leftrightarrow\ b^2-4ac>a^2\ \Leftrightarrow\ (p-20)^2=b^2>4ac+a^2=3200.0004[/TEX]

Les seul cas restant à traiter sont donc ceux où

...

par **benekire2** » 22 Déc 2009, 20:23

Je suis de retour de mon séjour sur la région parisienne ... Je vais me remettre sur l'exercice ( même si le dernier cas a traiter n'est franchement pas super simple ) .

par **benekire2** » 22 Déc 2009, 21:08

Je ne vois pas du tout comment y arriver, j'abandonne. Si t'as trouvé comment faire ben, je suis preneur, sinon, c'est pas grave !! Bonne soirée au forum.

par **Ben314** » 22 Déc 2009, 23:23

Pour le dernier cas (ou p est contenu dans un mouchoir de poche !!!)
je proposerais bien :
Etudier les fonctions p->x1 (qui dépend de p) et p->x2 (qui dépend de p) sur l'intervalle

en faisant les deux tableaux de variations (l'un en dessous de l'autre) avec en particulier les valeurs au bord de l'intervalle (que je te conseillerais de calculer à la machine...)
En regardant bien ces deux tableaux, tu devrais "voir" quand est-ce que l'intervalle contient un entier...

par **benekire2** » 23 Déc 2009, 09:38

Alors voilà ce que l'étude me donne:

x1 1414.213562 ==> croissante ==> 1414.713651
x2 1414.213562 ==> décroissante ==> 1413.713651

Et après, comment puis-je voir quand un entier se trouve entre les deux ?

parce que moi, je sais que l'intervalle contient un entier quand x2= 1414 et x1= 1414.427124
Donc, dois-je résoudre x2=1414 et en déduire les valeurs de p pour lesquelles l'intervalle contient un entier ? ?

( Toutes les valeurs sont arrondies ...)

Merci.

par **Ben314** » 23 Déc 2009, 10:52

C'est EXACTEMENT ça :
Vu les variations de x1 et x2 (et surtout les bornes), tu peut voir qu'au début, l'intervalle ne contient aucun entier, puis qu'à partir d'un certain moment, il se met à contenir l'entier 1414.
Et, effectivement, pour déterminer ce "moment" il suffit de résoudre x2=1414 qui te donnera la plus petite valeur de p pour laquelle l'intervalle contient l'entier 1414.

par **benekire2** » 23 Déc 2009, 13:06

ok, merci pour tout ben :)
Je n'ai plus qu'a conclure ( et aussi expliquer le fait que les deux fonctions sont symétriques par rapport à la droite d'équation y=...

par **Ben314** » 23 Déc 2009, 13:25

benekire2 a écrit:...les deux fonctions sont symétriques par rapport à la droite d'équation y=...

Je ne pense pas (car, vu le tableau, x1 augmente moins vite que x2 ne diminue...)

par **benekire2** » 23 Déc 2009, 13:48

ah mince ... j'avais bêtement conjecturer cela ... mais de toute manière on s'en fout, x1 reste dans les 1414 alors que x2 non, , enfin bref oublie la dernière remarque elle est inutile!!

par **ma_y_liss** » 23 Déc 2009, 17:21

Jpense pas que cela est à voir mais j'ai un petit problème sur les barycentres que je n'arrive pas à résoudre, si vous pouviez m'aider:

On considère quatre points A,B,C et D du plan.
Déterminer et construire l'ensemble des points M du plan tels que:
||MA+MB+MC||=||4MC-MD|| (ce sont des vecteurs ;))
merci beaucoup

par **benekire2** » 23 Déc 2009, 17:27

Effectivement cela n'a rien a voir ... c'est sur...

Alors, il va falloir que tu considère des barycentres ... tu poses G= Bar {(A1)(B1)(C1)} et G'=Bar{(C4)(D-1)} et par réduction, tu devrais tomber sur MG=M'G et donc en déduire que M est sur la médiatrice de [GG'].

Un problème dèrière quelque chose d'anodin

Qui est en ligne