J'ai quelques soucis avec un exercice sur les variables aléatoires.
Soit X une variable aléatoire dont la loi de probabilité est donnée par :
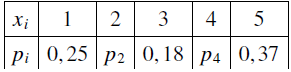
Déterminer les valeurs de
J'ignore si la formule
J'ai un tableau avec n=5 élément de X, aucune information sur k et p.
Quelle méthode de calcul dois-je employer pour trouver
A bientôt
