Petit problème dans une réccurence

[Pacha 54]

Bonjour
J'ai un DM de mathématiques dans lequel cet exercice est présent.
http://membres.lycos.fr/pacha541/Exercice%202%20DM.jpg
Or la question 2 me pose un petit problème. Pour démontrer l'inégalité j'utilise une démonstration par récurence que voici:
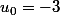
donc
donc
Ce qui prouve l'hérédité de la propriété...

Cependant après vérification, il n'est pas possible de diviser membre à membre deux inégalité voilà mon problème. Comment faut-il faire pour démontrer que ?
merci
@+

[lexot]

Bonjour

L'énoncé de ton devoir apparait une fois sur 2. Peux-tu l'insérer par un autre moyen?

Cordialement

[Flerendir]

Voila le bon lien

[url="http://img134.imageshack.us/img134/6637/dm9exercice2fy8.jpg"]http://img134.imageshack.us/img134/6637/dm9exercice2fy8.jpg[/url]

[Pacha 54]

Merci Flerendir. Sinon je l'ai mi sur mon serveur FTP http://membres.lycos.fr/pacha541/Exercice%202%20DM.jpg

[anima]

Bonjour
J'ai un DM de mathématiques dans lequel cet exercice est présent.
http://membres.lycos.fr/pacha541/Exercice%202%20DM.jpg
Or la question 2 me pose un petit problème. Pour démontrer l'inégalité j'utilise une démonstration par récurence que voici: (désolé je ne sais pas faire les indices)
u0=-3 donc u0 2uk-9>-7
donc (uk-8)/(2uk-9)<1
Ce qui prouve l'hérédité de la propriété...

Cependant après vérification, il n'est pas possible de diviser membre à membre deux inégalité voilà mon problème. Comment faut-il faire pour démontrer que u(k+1)<1?
merci
@+

J'ai bien une idée.
Perso, je supposerai que U_n tend vers -1. On a donc -9/-10, qui est inférieur à 1. Je l'ai fait avec une autre méthode sur brouillon, mais cette façon la (bien que rapide) est beaucoup plus rapide... :ptdr:

[Pacha 54]

J'ai bien une idée.
Perso, je supposerai que U_n tend vers -1. On a donc -9/-10, qui est inférieur à 1. Je l'ai fait avec une autre méthode sur brouillon, mais cette façon la (bien que rapide) est beaucoup plus rapide... :ptdr:

Bonsoir et merci de ta réponse. Mais la suite tend vers 1 et la convergence de la suite fait l'objet de la dernière question donc je ne pense pas que cette méthode soit valable dans cet exemple. Si tu veux bien m'expliquer la méthode que tu as utilisé sur ton brouillon je suis preneur, si celà ne te dérange pas.

Merci

[anima]

Je te réécris ça plus proprement:

Etape 2

or, Un < 1. On peut donc dire que:

Et donc dire que:
, prouvé

[anima]

Bonsoir et merci de ta réponse. Mais la suite tend vers 1 et la convergence de la suite fait l'objet de la dernière question donc je ne pense pas que cette méthode soit valable dans cet exemple. Si tu veux bien m'expliquer la méthode que tu as utilisé sur ton brouillon je suis preneur, si celà ne te dérange pas.

Merci

J'ai exprimé la suite en fonction de n, et non pas en fonction de l'antécédent. 3 pages de brouillon. Par contre, ensuite, la récurrence ça va tout seul :ptdr:

[Pacha 54]

Je te réécris ça plus proprement:

Etape 2

or, Un < 1. On peut donc dire que:

Et donc dire que:
, prouvé

Ok mais ce n'est pas
mais
Bon ca ne change pas grand chose pour la suite.
Par contre est tu sur que l'on peut diviser membre à membre 2 inégalités?
Après un doute avec Flerendir on a regardé sur wikipedia et on a pas trouver cette règle.

[Pacha 54]

J'ai exprimé la suite en fonction de n, et non pas en fonction de l'antécédent. 3 pages de brouillon. Par contre, ensuite, la récurrence ça va tout seul :ptdr:

lol bon ok les trois pages de brouillon on va eviter merci :ptdr:

[anima]

Ok mais ce n'est pas
mais
Bon ca ne change pas grand chose pour la suite.
Par contre est tu sur que l'on peut diviser membre à membre 2 inégalités?
Après un doute avec Flerendir on a regardé sur wikipedia et on a pas trouver cette règle.

Je n'ai pas divisé. J'ai posé une inégalité sur le numérateur, et une inégalité sur le dénominateur, et ensuite j'ai dit que la division d'une égalité sur l'autre entraine le résultat sur l'autre, et j'ai conclus.

P.S.: Si c'est 2un, je trouve 1 en quotient

[Pacha 54]

Je n'ai pas divisé. J'ai posé une inégalité sur le numérateur, et une inégalité sur le dénominateur, et ensuite j'ai dit que la division d'une égalité sur l'autre entraine le résultat sur l'autre, et j'ai conclus.

P.S.: Si c'est 2un, je trouve 1 en quotient

ok bon bin merci en faite si tu regarde bien mon premier post c'est ce que j'avais écrit mais le soucis s'était justement l'étape de la division.
par exemple 5<10 et 2<10 donc si on divise comme on le pensais 5/2<1 ce qui est faux.

[anima]

ok bon bin merci en faite si tu regarde bien mon premier post c'est ce que j'avais écrit mais le soucis s'était justement l'étape de la division.
par exemple 5<10 et 2<10 donc si on divise comme on le pensais 5/2<1 ce qui est faux.

Sauf que je n'ai rien divisé; j'ai remplacé.
On sait que Un aura comme valeur maxi 1. Donc, le numérateur de la suite aura comme valeur maximale -7 et le dénominateur comme valeur maximale -7 aussi. C'est du remplacement :we:

[Pacha 54]

Sauf que je n'ai rien divisé; j'ai remplacé.
On sait que Un aura comme valeur maxi 1. Donc, le numérateur de la suite aura comme valeur maximale -7 et le dénominateur comme valeur maximale -7 aussi. C'est du remplacement :we:

Comme dirais un amis que je connais bien (il se reconnaitra) "ouai, c'est pas faux".
ok bon bin on va faire ça comme ça merci.
Bonne soirée

[Flerendir]

oué c'est pas faux lol.

En effet Anima je pense qu'il faut raisonner comme ca, on est dans une démonstration par récurrence avec l'hypothèse de récurrence et pas
seulement dans une résolution d'inéquation.

Merci beaucoup!!

[lexot]

Bonjour

J'espère que tu pourras terminer!

Cordialement

[Pacha 54]

Bonjour

J'espère que tu pourras terminer!

Cordialement

C'est déja recopié pour moi :zen:
Merci à tous en tout cas, en particulier à Anima

[lexot]

Bonjour

Si 0
1 - > 0

Rectificatif

Si - 8 - 8) - - 9) > 0 ; et 1 - > 0

Cordialement