Bonjour à tous,
Mes maths sont bien loin derrière moi, aujourd'hui je suis un peu perdu quand il s'agit de remettre la main à la pâte, et je le dois pour un petit script dans un logiciel 3D.
Si quelqu'un peu m'aider ce serait bienvenue! Voici ma question :
Dans un repère orthonormé en 3 dimensions (o,X,Y,Z)
Je connais les coordonnées de 3 points A(x,y,z) , B(x,y,z) et C(x,y,z)
Soit P le plan qui passe pas ces 3 points.
Quel est la valeur de l'orientation (x y et z) de P dans le repère.
J'espère avoir été clair,
Merci.
Orientation d'un plan dans l'espace
7 messages
- Page 1 sur 1
Salut,
Je ne comprend pas la question :
Est ce que tu cherche une équation du plan passant par les 3 points ? (dans ce cas, le plus rapide est de voir que le produit vectoriel des vecteurs AB et AC fourni un vecteur normal du plan donc (presque) son équation)
Est ce que tu cherche comment orienter le plan, c'est à dire comment savoir si une base du plan est directe ou pas ? (dans ce cas, il n'y a pas de réponse car tu peut choisir l'orientation que tu veut : intutivement, cela revient à dire que l'on peut regarder le plan soit d'un coté, soit de l'autre...)
Je ne comprend pas la question :
Est ce que tu cherche une équation du plan passant par les 3 points ? (dans ce cas, le plus rapide est de voir que le produit vectoriel des vecteurs AB et AC fourni un vecteur normal du plan donc (presque) son équation)
Est ce que tu cherche comment orienter le plan, c'est à dire comment savoir si une base du plan est directe ou pas ? (dans ce cas, il n'y a pas de réponse car tu peut choisir l'orientation que tu veut : intutivement, cela revient à dire que l'on peut regarder le plan soit d'un coté, soit de l'autre...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La notion d'angle entre un plan P et une droite D n'est pas trés utilisé en math.
Je suppose que cet angle est celui entre D et l'intersection de P avec le plan perpendiculaire à P contenant D (c'est le plus petit angle entre D et une droite du plan).
Dans ce cas, il vaut 90° moins l'angle entre D et la normale au plan, et comme on peut calculer (produit vectoriel) un vecteur normal au plan on obtient le résultat assez facilement :
On calcule (produit vectoriel) et on trouve
(produit vectoriel) et on trouve ) .
.
L'angle du plan avec l'axe des
du plan avec l'axe des  (dirigé par
(dirigé par ) ) vérifie alors :
) vérifie alors :
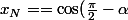||\vec{i}||\,||\vec{N}||=\sin(\alpha)\sqrt{x_N^2+y_N^2+z_N^2}) donc
donc 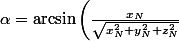)
Idem pour les deux autres axes.
Je suppose que cet angle est celui entre D et l'intersection de P avec le plan perpendiculaire à P contenant D (c'est le plus petit angle entre D et une droite du plan).
Dans ce cas, il vaut 90° moins l'angle entre D et la normale au plan, et comme on peut calculer (produit vectoriel) un vecteur normal au plan on obtient le résultat assez facilement :
On calcule
L'angle
Idem pour les deux autres axes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, car une des définitions (équivalentes) de l'angle entre deux plans est de prendre l'angle entre des vecteurs normaux aux plans
donc l'angle entre P et le plan (YZ) est l'angle entre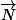 et
et  : par rapport à ce qu'il y a dans le premier post, cela revien à ne pas prendre
: par rapport à ce qu'il y a dans le premier post, cela revien à ne pas prendre  mais directement
mais directement  .
.
donc l'angle entre P et le plan (YZ) est l'angle entre
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
