Leo M a écrit:Pouvez-vous m'aider?
non, on ne peut pas. :zen:
le centre du cercle circonscrit a la joie de vous annoncer
qu'il est actuellement au point de concours de deux médiatrices,
et ce , pour une durée indéterminée.
Comme les médiatrices sont des ensembles de points équidistants
des extrêmités du segment, les affixes de leurs points vérifient:
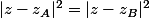
mais
le carré d'un module s'écrit agréablement comme le produit du complexe et de son complexe conjugué.d'où il vient les équations:
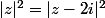
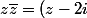(\bar{z}+2i))
de plus, en utilisant une formule dûe à léonhard Euler, immense mathématicien
suisse du 18 ème siècle:
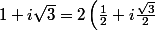 = 2 e^{i \frac{\pi}{3}})
chacun sait en effet que le cos(60°) vaut
l'exponentielle est un complexe de module 1: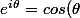+i sin(\theta))
finalement, tu devrais trouver un système 2x2
deux équations, deux inconnues des affixes
et
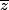
car il y a deux médiatrices.
tu peux résoudre ce système par la méthode des combinaisons linéaires
ou par la méthode de substitution:
 = -4 \\<br />ze^{ - i \frac{\pi}{3}}+\bar{z}e^{ i \frac{\pi}{3}}=2)
