Nombres complexes

par **MacErmite** » 03 Fév 2007, 18:34

Bonjour à tous,

Pouvez-vous m'aider sur un petit problème concernant le travail sur les nombres complexes ?

Voilà, l'on suppose l'existence de trois points A, B et C définis comme suit :

le point A a pour affixe z, le point B aura B(i) et C (iz). Comment définir A afin de les aligner ?

Pour le moment j'ai trouvé cette relation, avec A: z=a+ib :

après je vois pas comment "redéfinir" A ?

par **anima** » 03 Fév 2007, 18:43

MacErmite a écrit:Bonjour à tous,

Pouvez-vous m'aider sur un petit problème concernant le travail sur les nombres complexes ?

Voilà, l'on suppose l'existence de trois points A, B et C définis comme suit :

le point A a pour affixe z, le point B aura B(i) et C (iz). Comment définir A afin de les aligner ?

Pour le moment j'ai trouvé cette relation, avec A: z=a+ib : après je vois pas comment "redéfinir" A ?

Je le définirai plutôt en forme exp, perso.
A: re^(iT)
B: e^(ipi/2)
C: e^(ipi/2)*re^(iT) = re^(i(pi/2+T))

Or, A, B et C sont alignés si et seulement si la valeur absolue de leur argument est la même.
|iT| = |ipi/2| = |i(pi/2+T)|
C'est une façon de voir les choses :++:

par **rene38** » 03 Fév 2007, 18:48

Bonjour

A, B, C sont alignés si et seulement si

et

sont colinéaires.

par **allomomo** » 03 Fév 2007, 18:57

Salut,

Homothétie

avec

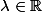
En Complexe :

et on va avoir

par **MacErmite** » 03 Fév 2007, 19:06

rene38 a écrit:Bonjour

A, B, C sont alignés si et seulement si et sont colinéaires.

C'est ainsi que j'ai trouvé

j'ai noté A(a,b); B(0,1) et C(-b,a) (Pour C j'ai multiplié a+ib par i). Ensuite les vecteurs CB et CA étant colinéaires le determinant est égal à zéro.

par **rene38** » 03 Fév 2007, 19:16

Restons plutôt chez les complexes :
A(z) ; B(i) et C(iz) donc

et

sont colinéaires ssi

,

ou

,

et on traduit en utilisant les affixes des vecteurs.

par **MacErmite** » 03 Fév 2007, 19:35

rene38 a écrit:Restons plutôt chez les complexes :
A(z) ; B(i) et C(iz) donc et

et sont colinéaires ssi , ou ,

et on traduit en utilisant les affixes des vecteurs.

Toutes ces solutions sont intéressantes. Pour cette dernière j'ai trouvé :

Nombres complexes

nombres complexes

Qui est en ligne