Bonjour à tous,
J'ai un exercice à faire pour demain sur les nombres complexes, il s'agit d'un vrai ou faux et il s'avère que j'ai des doutes sur deux questions:
1) L'inverse de (2+3i)/(5-i) est 2+i
2) i^27 est un nombre réel
Merci d'avance pour vos réponses
Nombres complexes
8 messages
- Page 1 sur 1
Re: Nombres complexes
Salut,
1) L'inverse de A/B, c'est B/A et B/A, c'est égal à C si et seulement si B=AC.
2) Complète :
Qu'est-ce que tu en pense ? En particulier, ça vaut combien ?
?
1) L'inverse de A/B, c'est B/A et B/A, c'est égal à C si et seulement si B=AC.
2) Complète :
Qu'est-ce que tu en pense ? En particulier, ça vaut combien
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Nombres complexes
1) Je ne pas trop compris..
ce que j'ai essayé de faire pour la 1) c'est de mettre (2+3i)/(5-i) sous forme a+bi et après de faire 1/a+bi
2)
i^2=-1, i^3=-i, i^4=1, i^5=i, i^6=-1, i^7=-i, i^8=1, i^9=i
Ce que je vois c'est qu'à chaque fois y a "-1, -i, 1, i" et que i^27=-i
ce que j'ai essayé de faire pour la 1) c'est de mettre (2+3i)/(5-i) sous forme a+bi et après de faire 1/a+bi
2)
i^2=-1, i^3=-i, i^4=1, i^5=i, i^6=-1, i^7=-i, i^8=1, i^9=i
Ce que je vois c'est qu'à chaque fois y a "-1, -i, 1, i" et que i^27=-i
Re: Nombres complexes
Pour le 1), tu peut faire comme ça : c'est pas mal plus long que ce que je te proposait, mais ça permet de s'entrainer à faire des calculs.
Tu trouve quoi pour a+bi ?
Pour le 2), c'est bon : effectivement i^27=-i (et ce n'est donc pas un nombre réel).
Est-ce que tu vois une façon de l'expliquer autre que de dire "au vu du tableau, on voit bien que i^27=-i".
A mon avis, c'est déjà très bien, mais le prof. risque de considérer que c'est pas suffisant comme explication (les "on voit bien que", on considère souvent en math que c'est pas vraiment une preuve...)
Tu trouve quoi pour a+bi ?
Pour le 2), c'est bon : effectivement i^27=-i (et ce n'est donc pas un nombre réel).
Est-ce que tu vois une façon de l'expliquer autre que de dire "au vu du tableau, on voit bien que i^27=-i".
A mon avis, c'est déjà très bien, mais le prof. risque de considérer que c'est pas suffisant comme explication (les "on voit bien que", on considère souvent en math que c'est pas vraiment une preuve...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Nombres complexes
Merci pour votre réponse.
J'ai trouvé( 7/26)+(17/26i), et enfin pour l'inverse j'ai trouvé ( 7/26)-(17/26i)/0,5
J'ai trouvé( 7/26)+(17/26i), et enfin pour l'inverse j'ai trouvé ( 7/26)-(17/26i)/0,5
Re: Nombres complexes
2) Je dirai que i^27=-i, et que -i=-√-1 donc ce n'est pas réel car -√-1 n'existe pas dans R
Re: Nombres complexes
Oui, c'est ça, modulo que le dernier truc, ça serait plus "standard" de l'écrire 7/13-17/13i.
Sinon, ce que je te proposait, c'est de commencer par dire que l'inverse de c'est évidement égal à
c'est évidement égal à  puis que, de dire que
puis que, de dire que  , ça revient exactement à dire que
, ça revient exactement à dire que 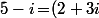(2+i)) .
.
Donc il suffit de calculer le produit(2+i)) et de regarder si ça donne ou pas 5-i et c'est plus rapide que de faire des divisions.
et de regarder si ça donne ou pas 5-i et c'est plus rapide que de faire des divisions.
Sinon, pour le 2), je pense que le plus simple pour "bien expliquer tout comme il faut", c'est de partir de i^4=1 et d'en déduire que i^(24)=i^(4x6)=(i^4)^6=1^6=1 puis que i^27=i^(24+3)=i^24xi^3=1xi^3=i^3 (mais il y a bien sûr d'autres méthodes)
EDIT : j'avais pas vu ton post : évite comme la peste d'écrire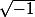 : dans R, ça n'existe pas et dans C, c'est pas clair du tout de savoir ce que ça vaut vu qu'il y a deux complexe dont le carré fait -1 qui sont i et -i et on sait pas lequel des deux ça désigne.
: dans R, ça n'existe pas et dans C, c'est pas clair du tout de savoir ce que ça vaut vu qu'il y a deux complexe dont le carré fait -1 qui sont i et -i et on sait pas lequel des deux ça désigne.
Sinon, ce que je te proposait, c'est de commencer par dire que l'inverse de
Donc il suffit de calculer le produit
Sinon, pour le 2), je pense que le plus simple pour "bien expliquer tout comme il faut", c'est de partir de i^4=1 et d'en déduire que i^(24)=i^(4x6)=(i^4)^6=1^6=1 puis que i^27=i^(24+3)=i^24xi^3=1xi^3=i^3 (mais il y a bien sûr d'autres méthodes)
EDIT : j'avais pas vu ton post : évite comme la peste d'écrire
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
