Nombres complexes

[Lola.Rose77]

Bonjour,
J'ai un dm à rendre bientôt mais je bloque sur un exercice. J'ai déjà commencé à le faire mais je ne suis sûr de rien alors j'aimerai avoir un peu d'aide. Je vous remercie d'avance pour cela !

Déterminer dans chaque cas l'ensemble des points M(z) pour lesquels M'(z') appartient à l'axe réel :
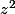
1) z'= -2z
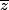
2) z' = ( -3)(iz+1)
3) z' = i

Je sais que pour que z' soit réel il faut que sa partie imaginaire soit =0
Je pense aussi qu'il faut remplacer z par x+iy avec x et y réels
dans le 1) par ex j'obtiens x=-1 et b=0et dans le 2) x=3 ou x=0
Est -ce que c'est bon ?
Mais pour le 3) je ne sais pas du tout ...

[zygomatique]

Bonjour,
J'ai un dm à rendre bientôt mais je bloque sur un exercice. J'ai déjà commencé à le faire mais je ne suis sûr de rien alors j'aimerai avoir un peu d'aide. Je vous remercie d'avance pour cela !

Déterminer dans chaque cas l'ensemble des points M(z) pour lesquels M'(z') appartient à l'axe réel :
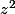
1) z'= -2z
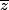
2) z' = ( -3)(iz+1)
3) z' = i

Je sais que pour que z' soit réel il faut que sa partie imaginaire soit =0
Je pense aussi qu'il faut remplacer z par x+iy avec x et y réels
dans le 1) par ex j'obtiens x=-1 et b=0et dans le 2) x=3 ou x=0
Est -ce que c'est bon ?
Mais pour le 3) je ne sais pas du tout ...

salut

z' est réel

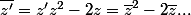
on met tout dans un membre et on factorise ....

idem pour les autres ....

[mathelot]

bonjour,

i) ou la droite verticale d'équation x=1

ii) l'origine O(0,0)


3) cercle centré en l'origine de rayon 1


-------------
j'ai démarré avec les équivalences



et

[mathelot]

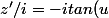pour la (3) poser avec

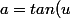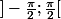
le changement de variable est bijectif de sur , mais après , quand tu calcule z, ça s'arrange.

[paquito]

Pour la 3) soit M(z), A(1) et B(-1); ensuite , d'où est réel imaginaire pur donc .

Mais
caractérise le cercle de diamètre [AB] privé du point A

[Lola.Rose77]

Merci pour toutes vos réponses, j'ai réussi à finir l'exercice grâce à vous :we:

[mathelot]

pour la (3) ,autre méthode

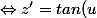z' réel avec








d'où cercle centré en l'origine, de rayon 1, privé de B(1).

[zygomatique]

en notant z* le conjugué de z

3/

z' est réel <==> i(z + 1)(1 - z*) = -i(z* + 1)(1 - z) <==> 1 - z* + z - zz* = -1 - z* + z + zz* <==> zz* = 1 <==> ....


avec z <> 1 bien sur ...