DM nombres complexes

[knock]

Bonjour a tous ,
J'ai une question a propos d'un exercice que je n'arrive pas a terminé. Voici l'énoncé :
V=racine carré
En utilisant la forme exponentielle, donner la forme algébrique du nombre complexe : (-1+i)^4×(6+3iV(3))^6
Donc j'ai réussi a mettre sous forme exponentielle (-1+i)^4 qui donne 4e^(i pi).Mais je n'arrive pas a mettre sous forme exponentielle (6+3iV(3))^6 qui me donne des résultats impossible. Donc ma question est comment puis je faire pour le mettre sous forme exponentielle :hein: .
Merci d'avance :we:

[mathelot]

factorise par

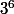
[knock]

C'est a dire ? :hein:

[mathelot]

es tu sûr de ton énoncé ? ça ne donne pas des valeurs remarquables pour les lignes trigonométriques des angles polaires.

[knock]

Je viens de vérifier et l'énoncé est bon. Et comme ces sur un livre de maths peut être qu'il est faux ? :hein:

[mathelot]

à ce stade , deux possibilités:
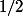
- modifier l'énoncé pour faire apparaitre les valeurs habituelles et
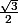
- ne pas modifier l'énoncé et utiliser la formule du binome:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1

[knock]

Merci de ta réponse, mais je n'ai pas encore étudié le binôme de newton , donc je pense qu'il y a une faute dans l'exercice. :)

[Le Chat]

Merci de ta réponse, mais je n'ai pas encore étudié le binôme de newton , donc je pense qu'il y a une faute dans l'exercice.

Non, non :ptdr:
Il y a d'autres méthodes pour développer ce genre d'expressions comme la formule de De Moivre

[knock]

J'ai essayer avec la formule de Demoivre et cela ne marche pas ? Il y d'autre méthodes :)

[mathelot]

si , posons

puis