Nombres complexes, équation et écriture trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
charly45
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Mar 2010, 13:07
-
 par charly45 » 09 Oct 2010, 10:25
par charly45 » 09 Oct 2010, 10:25
Bonjours,
Pouvez-vous m'aider à résoudre cet exercice ?
Soit (E) l'équation :
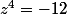
a) Calculer
^2^}{2})
b) En déduire les solutions de (E).
c) Donner une écriture trigonométrique des ces solutions.
Mes réponses :
a)
^2^}{2} = i)
b)
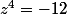
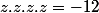
(x+iy)(x+iy)(x+iy) = -12)
(x^2+ixy-y+ixy) = -12)
(x^2-y+2ixy) = -12)

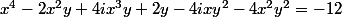
+i(4x^3y-4xy^2) = -12)
-12 est un réel, donc
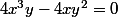
donc
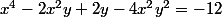
Comment en déduire les solutions de (E) ?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 09 Oct 2010, 11:00
par annick » 09 Oct 2010, 11:00
Bonjour,
moi, j'aurai bien essayé une piste du genre :
-12=12 i²=(12)[(1+i)/2]²
-
nadine93
- Messages: 7
- Enregistré le: 23 Sep 2012, 18:41
-
 par nadine93 » 07 Oct 2012, 21:09
par nadine93 » 07 Oct 2012, 21:09
en élevant au carré l'égalité (1+i)²/2=i on trouve (1+i)^4/4=i²=-1 et en multipliant cette égalité par 12 on obtient: 3(1+i)^4=-12 ce qui prouve que la racine 4ième de 3 multipliée par 1+i est une solution de l'équation (E) qu'on peut noté U
Pour trouver maintenant toutes les solutions de (E) on a : (Z/u)^4=1 , on se ramène alors aux racines quatrièmes de l'unité ......
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 114 invités
