Nombres complexes et application à la géométrie

[Elo63]

Bonsoir à tous je bloque un peu sur la réponse que l'on m'a donnée d'un exercice. En fait je ne la comprends pas très bien alors si quelqu'un veut bien m'expliquer ...

Le plan complexe est rapporté à un repère orthonormal direct (O,u,v). On considère le point A d'affixe 1 et, pour tout (théta)appartenant à [0;2pi], le point M d'affixe z=e puissance(ithéta). On désigne par P le point d'affixe 1+z et par Q le point d'affixe z².
Voilà ça c'est le début de l'énoncé et plus loin on me dit :
Soit S le point d'affixe 1+z+z², où z désigne toujours l'affixe du point M.

Et enfin l'ultime question avec la réponse que je ne comprends pas :
4. Dans le cas où S est différent de 0, tracer la droite (OS). Quelle conjecture apparaît, relativement au point M ? Démontrer que le nombre (1+z+z²)/z est réel, quel que soit théta appartenant à [0;2pi[. Conclure sur la conjecture précédente.

On "voit" sur la figure que M est sur la droite (OS).

Multiplions (1+z+z²)/z par z_ (z barre), afin de faire disparaître le complexe au dénominateur :

(1+z+z²).z_/zz_

On a (1+z+z²).z_=(1+eiq+ei2q).ei-q=ei-q+1+eiq=1+2cosq, qui est réel.

Le dénominateur étant réel, (1+z+z²)/z est réel.

On en conclue que OS est colinéaire à OM, et donc que M appartient à (OS)
q= théta

Je ne comprends pas très bien, enfin je comprends pourquoi on multiplie par z barre (en effet le produit de z et z barre donne un nombre réel et ensuite il faut s'occuper du numérateur et je bloque)

Merci d'avance de votre aide. :ptdr:

[Sa Majesté]

Bonsoir,
Où bloques-tu exactement ?

[Luc]

Bonsoir,

la conjecture qui apparaît est comme tu le dis que les points O, M et S sont alignés, et ce quelque soit z. L'objet de la question 4 est de le montrer.
As-tu vu dans ton cours que si tu as trois points A, B, C, distincts, d'affixe respective , et 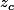, alors ils sont alignés si et seulement si le rapport est réel?. De façon plus précise, l'argument de ce rapport est une mesure de l'angle orienté . Et si A,B,C sont alignés, ces vecteurs sont colinéaires, et l'angle orienté vaut donc ou . Alors est réel car son argument vaut (cas où le réel est positif) ou (cas ou le réel est négatif). C'est ce qui se passe dans ton exercice.

Dans ton exercice, les trois points sont O, M et S.
Est-ce que tu comprends comment on montre que le quotient est réel?

Pour montrer qu'une fraction complexe est réelle, on commence le plus souvent par multiplier en haut et en bas pas le complexe conjugué du dénominateur. Comme ça, le dénominateur est réel, est on se ramène alors à montrer qu'un certain nombre complexe est réel.