Dm de math
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 17:49
par titine » 14 Sep 2014, 17:49
Qu'as tu trouvé pour f(-1) ? Pour f'(x) ? Pour f'(-1) ?
 par shitrolololoeasy » 14 Sep 2014, 17:51
par shitrolololoeasy » 14 Sep 2014, 17:51
titine a écrit:Qu'as tu trouvé pour f(-1) ? Pour f'(x) ? Pour f'(-1) ?
f(-1) = 3
f'(-1) = 0
et f(x) je c'est pas le dériver vu que ya pas de chiffres ya que des a , b et c
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 17:52
par titine » 14 Sep 2014, 17:52
shitrolololoeasy a écrit:je n'arrive pas a dériver la fonction
Dérivée de x² ?
Dérivée de 5x² ?
Dérivée de ax² ?
Dérivée de 1/x ?
Dérivée de b/x ?
 par shitrolololoeasy » 14 Sep 2014, 17:54
par shitrolololoeasy » 14 Sep 2014, 17:54
titine a écrit:Dérivée de x² ?
Dérivée de 5x² ?
Dérivée de ax² ?
Dérivée de 1/x ?
Dérivée de b/x ?
dérivée de 5x² = 10x
dérivée de ax2 = 2ax
dérivéz de 1/x = -1/x²
et le dernier che pas
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 17:58
par titine » 14 Sep 2014, 17:58
Dérivée de 1/x = -1/x²
Donc la dérivée de b/x c'est à dire de b*1/x est b*-1/x² = -b/x²
Et donc f'(x) = ?
 par shitrolololoeasy » 14 Sep 2014, 18:00
par shitrolololoeasy » 14 Sep 2014, 18:00
titine a écrit:Dérivée de 1/x = -1/x²
Donc la dérivée de b/x c'est à dire de b*1/x est b*-1/x² = -b/x²
Et donc f'(x) = ?
3ax² + b / 3x ??
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 18:12
par titine » 14 Sep 2014, 18:12
shitrolololoeasy a écrit:3ax² + b / 3x ??
Je ne comprends pas.
On a dit que la dérivée de b/x est -b/x²
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 18:14
par Shew » 14 Sep 2014, 18:14
Et
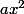
a pour dérivé
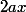
 par shitrolololoeasy » 14 Sep 2014, 18:20
par shitrolololoeasy » 14 Sep 2014, 18:20
Shew a écrit:Et
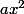
a pour dérivé
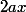
a oui désoler enfete sans me rendre conte je regarder le mauvais exo du coup je dériver pas la bonne
ça donne donc 2ax - b/x²
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 18:29
par titine » 14 Sep 2014, 18:29
Ok
Alors on a :
f(x) = ax² + b/x et f'(x) = 2ax - b/x²
Donc comme f(-1) = 3 alors a(-1)² + b/(-1) = 3. Donc a - b = 3
Et comme f'(-1) = 0 alors 2a(-1) - b/(-1)² = 0. Donc -2a - b = 0
Pour trouver a et b tu résous le système :
a - b = 3
-2a - b = 0
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 18:35
par titine » 14 Sep 2014, 18:35
shitrolololoeasy a écrit:a oui désoler enfete sans me rendre conte je regarder le mauvais exo du coup je dériver pas la bonne
ça donne donc 2ax - b/x²
en faite c'est la fête de dériver !
C'est presque aussi excitant qu'un conte des milles et une nuits !
Je plaisante !!
 par shitrolololoeasy » 14 Sep 2014, 18:45
par shitrolololoeasy » 14 Sep 2014, 18:45
titine a écrit:Ok
Alors on a :
f(x) = ax² + b/x et f'(x) = 2ax - b/x²
Donc comme f(-1) = 3 alors a(-1)² + b/(-1) = 3. Donc a - b = 3
Et comme f'(-1) = 0 alors 2a(-1) - b/(-1)² = 0. Donc -2a - b = 0
Pour trouver a et b tu résous le système :
a - b = 3
-2a - b = 0
merci beaucoup pour ton aide je me douche et je résous ça :we:
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 14 Sep 2014, 20:10
par titine » 14 Sep 2014, 20:10
shitrolololoeasy a écrit:je trouve a = 1 et b = -2 c'est bon ?
Oui c'est bon
 par shitrolololoeasy » 14 Sep 2014, 20:17
par shitrolololoeasy » 14 Sep 2014, 20:17
titine a écrit:Oui c'est bon
pour la 2 a je fait les limites de f(x) sur -infini , 0 et + infini c'est ça ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 20:29
par Shew » 14 Sep 2014, 20:29
shitrolololoeasy a écrit:pour la 2 a je fait les limites de f(x) sur -infini , 0 et + infini c'est ça ?
Pas sur 0 puisque
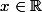
\{0}
 par shitrolololoeasy » 14 Sep 2014, 20:48
par shitrolololoeasy » 14 Sep 2014, 20:48
Shew a écrit:Pas sur 0 puisque
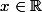
\{0}
merci pour ton aide j'aurais pas réussi sans toi
 par shitrolololoeasy » 15 Sep 2014, 17:46
par shitrolololoeasy » 15 Sep 2014, 17:46
en faite il fallait faire en 0 aussi la prof me la dit .
je comprend pas la 3 vous pouvez m'aidez svp ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Sep 2014, 17:54
par Shew » 15 Sep 2014, 17:54
shitrolololoeasy a écrit:en faite il fallait faire en 0 aussi la prof me la dit .
je comprend pas la 3 vous pouvez m'aidez svp ?
????
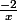
n'est pas defini en x = 0 ou même si x tend vers 0 donc je ne vois pas l'interet de calculer une limite incalculable .... :hum: . Apparement cette question servira pour en déduire l'asymptote bref ...
Pour la 3a comme vous connaissez les valeurs de a et b; écrivez f' et ramenez tout au même dénominateur puis développez l'expression de la question 3a et comparez .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
