Majorant

[mimix]

bonjour,
pourquoi un majorant M peut-il être inférieur ou égale à un élément d'une partie non vide A?
quelquesoit x appartenant à A, pourquoi a-t-on x << M, M= supA.

par définition, un majorant est un élément supérieur à tous les éléments de cette partie, et est supérieure au maximum non? ? merci

[Nightmare]

Salut,

Plusieurs définitions :

Etant donnée une partie A d'un ensemble E, on définit :

Un majorant de A : C'est un élément de E supérieur à tous les éléments de A. Littéralement, est un majorant de A si et ssi pour tout élément ,

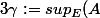La borne supérieure de A : c'est le plus petit des majorants de A (dans E), pourvu qu'il existe. Mathématiquement, on a deux informations qui le caractérise. La première est que c'est un majorant, donc pour tout x dans A, (). La deuxième est que c'est le plus petit des majorants, ce qui peut se traduire en disant que si l'on choisit un nombre inférieur à la borne sup, ce ne peut être un majorant, donc pour tout 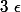positif, il existe un x dans A tel que .
Ceci donne peut être un sens à "x << M" bien que j'ai du mal à voir ce que pourrait signifier ici le symbole <<.

Le maximum de A : C'est le plus grand élément de A. Il est clair que si A admet un maximum, c'est aussi sa borne sup dont le plus petit des majorants, ce qui répond à ta dernière question.