Limites Term
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Abysson
- Messages: 3
- Enregistré le: 29 Déc 2009, 00:16
-
 par Abysson » 29 Déc 2009, 00:31
par Abysson » 29 Déc 2009, 00:31
Bonjour,
J'ai un problème au niveau d'une limite a cas indeterminé, je n'arrive pas a la factoriser et a la finir.
Voici le problème :
- Code: Tout sélectionner
(x)=(2x)/(Racine(x²-4))
Df = ]-Infini ; -2[ U ]2 ; +Infini[
Je dois trouver donc les limites de cette fonction :
- Code: Tout sélectionner
lim = (2x)/(Racine(x²-4)) = - Infini / + Infini
x->-Infini
Et la j'arrive pas a venir a bout de ma factorisation
Merci de votre aide

-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 29 Déc 2009, 00:37
par Skullkid » 29 Déc 2009, 00:37
Bonsoir, ce type de limites en l'infini se traitent comme celles des fractions rationnelles : il faut factoriser le numérateur et le dénominateur par la plus grande puissance de x qui y figure.
Ici, la racine carrée pose problème, mais on peut tout de même y arriver : commence par factoriser ce qui se trouve sous la racine par une puissance de x bien choisie, et fais sortir cette puissance de x de la racine (en faisant attention au signe de x, selon que tu te trouves en

ou

).
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2009, 03:51
par Dinozzo13 » 29 Déc 2009, 03:51
Salut !
Tu as une fonction

définie sur

par
=\frac{2x}{\sqrt{x^2-4}})
.
Fait ensuite comme il t'a été dit :
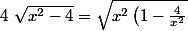}=|x|\sqrt{1-\frac{4}{x^2}}=\left\{<br />\begin{array}<br />x\sqrt{1-\frac{4}{x^2}} si x\in]2;+ \infty[ \\<br />ou \\<br /> - x\sqrt{1-\frac{4}{x^2}} si x\in]-\infty;-2[<br />\end{array}<br />\right)
.
Déduis-en

En espérant t'avoir aidé.
-
Abysson
- Messages: 3
- Enregistré le: 29 Déc 2009, 00:16
-
 par Abysson » 29 Déc 2009, 11:27
par Abysson » 29 Déc 2009, 11:27
Merci beaucoup !
Je savais qu'il fallait factoriser avec x mais je n'y arrivai pas a la racine, je serai encore bloqué surement ^^
Sur ce, a la prochaine ;)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 29 Déc 2009, 11:28
par benekire2 » 29 Déc 2009, 11:28
et comme tu fais tendre vers -infini ca donne |x|=-x
et ensuite tu simplifie par x ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
