Limites de suite (TS)

par **ptite fleure** » 13 Sep 2007, 18:44

Bonjour,
J'explique mon problème :

J'ai réussi à démontrer que pour tt n E N, Un > ou égal à 0 alors l > ou égal à 0 ms lorsque Un>0 peut on dire que l >0 ? et si l > 0 que peut t'on dire du signe des termes de la suite et comment le prouver ?

Pour finir, est ce que vous seriez me dire comment montrer que (racine de x+1) moins (racine de x) n'est pas dérivable en 0? J'essaie avec le taux de variation t(h) mais je m'en sors pas vraiment.

Je vous remercie vraiment vraiment beaucoup de m'aider, je vous en serez TRES reconnaissante :we:

par **Nightmare** » 13 Sep 2007, 18:51

Bonjour,

Oui, si U(n) est positive, la limite l ne peut être négative.

Si l > 0 alors les U(n) sont positifs a partir d'un certain rang

Pour la deuxième question.

Tu as pour h au voisinage de 0 l'approximation affine (vue en première) :

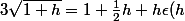avec epsilon une fonction qui converge vers 0 lorsque h tend vers 0
On a alors :

Malheureusement, à cause du 1/h ce rapport diverge quand h tend vers 0. La fonction n'est donc pas dérivable en 0

par **ptite fleure** » 13 Sep 2007, 18:55

Merci bcp ! cependant je comprends tes réponses mais pour les limites de suites j'arrive pas à les prouver...
et j'ai pas trop compris pour le epsillon.
Dsl de te déranger et encore merci :++:

par **Monsieur23** » 13 Sep 2007, 18:56

Précision : Si les u_n sont strictements positifs, alors la limite l si elle existe est positive OU NULLE

Exemple :

par **ptite fleure** » 13 Sep 2007, 19:07

Me laisser pas svp..

par **Nightmare** » 13 Sep 2007, 19:13

Autre méthode peut être plus compréhensive :

(quantité conjuguée)

Simplifie et fait tendre h vers 0, le résultat est direct.

par **Monsieur23** » 13 Sep 2007, 19:14

Tu pourrais par exemple calculer la limite du taux d'accroissement

Edit : Trop tard

par **ptite fleure** » 13 Sep 2007, 19:17

d'accord j'ai compris ! Et c'est quoi la conséquence sur l'interprétaion graphique car je vois pas du tout ...

par **Nightmare** » 13 Sep 2007, 19:18

Ben regarde la tête de ta tangente à la courbe au point d'abscisse x=0...

par **ptite fleure** » 13 Sep 2007, 19:21

ben justement je vois aps ce que ca donne..

par **Nightmare** » 13 Sep 2007, 19:24

Une tangente verticale non?

par **ptite fleure** » 13 Sep 2007, 19:32

asymptote verticale c'est pareil ?

par **ptite fleure** » 13 Sep 2007, 19:37

C'est comme une asymptote verticale ?

par **ptite fleure** » 13 Sep 2007, 19:39

Dsl j'ai envoyer deux fois pareil :hum:

par **Nightmare** » 13 Sep 2007, 19:46

Non, tangente et asymptote ce n'est pas la même chose.

par **ptite fleure** » 13 Sep 2007, 19:51

ok je vois pas trop pourquoi mias bon merci

par **Nightmare** » 13 Sep 2007, 19:55

C'est parce que ce n'est pas la même définition tout simplement.

Une tangente c'est une droite qui vient couper la courbe en un point orthogonalement. Une asymptote c'est une droite vers laquelle la courbe va se rapprocher infiniment, ce n'est quand même pas la même chose !

par **ptite fleure** » 14 Sep 2007, 18:20

ok merci !

Limites de suite (TS)

Limites de suite (TS)

Qui est en ligne