Limite logarithmique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 28 Jan 2012, 14:01
par Dante0 » 28 Jan 2012, 14:01
Bonjour,
Comment trouver la limite suivante :
}{lnx})
quand x tend vers +oo ?
Merci !
-
kiosquamuffins
- Membre Naturel
- Messages: 13
- Enregistré le: 27 Jan 2012, 19:10
-
 par kiosquamuffins » 28 Jan 2012, 14:27
par kiosquamuffins » 28 Jan 2012, 14:27
Dante0 a écrit:Bonjour,
Comment trouver la limite suivante :
}{lnx})
quand x tend vers +oo ?
Merci !
Bonjour,
Si tu devais calculer la limite de ln(y)/y quand y tend vers l'infini, comment ferais-tu ?
Il te suffit alors de poser y=ln(x) qui tend bien vers l'infini quand x tend vers l'infini et tu as ta réponse.
Tu comprends ?
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 28 Jan 2012, 16:30
par geegee » 28 Jan 2012, 16:30
Dante0 a écrit:Bonjour,
Comment trouver la limite suivante :
}{lnx})
quand x tend vers +oo ?
Merci !
Bonjour,
ln( lnx) tend vers +infini moins que lnx donc limite(e->infini)
}{lnx})
=0
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 30 Jan 2012, 17:12
par Dante0 » 30 Jan 2012, 17:12
kiosquamuffins a écrit:Bonjour,
Si tu devais calculer la limite de ln(y)/y quand y tend vers l'infini, comment ferais-tu ?
Il te suffit alors de poser y=ln(x) qui tend bien vers l'infini quand x tend vers l'infini et tu as ta réponse.
Tu comprends ?
Pas vraiment. On tombe sur une forme indéterminée en gros puisque le haut et le bas tendent vers +oo
Je peux pas utiliser le théorème de l'hopital ici ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 30 Jan 2012, 17:39
par Sylviel » 30 Jan 2012, 17:39
normalement tu sais calculer la limite ln(y)/y, non ? (c'est dans le cours a priori).
Et le changement de variable permet de t'y ramener.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 30 Jan 2012, 18:57
par el niala » 30 Jan 2012, 18:57
Dante0 a écrit:Pas vraiment. On tombe sur une forme indéterminée en gros puisque le haut et le bas tendent vers +oo
Je peux pas utiliser le théorème de l'hopital ici ?
la règle de l'Hospital est au programme de Terminale ? J'ai la flemme de regarder, mais il me semble que non, non ?
-
kiosquamuffins
- Membre Naturel
- Messages: 13
- Enregistré le: 27 Jan 2012, 19:10
-
 par kiosquamuffins » 30 Jan 2012, 20:33
par kiosquamuffins » 30 Jan 2012, 20:33
el niala a écrit:la règle de l'Hospital est au programme de Terminale ? J'ai la flemme de regarder, mais il me semble que non, non ?
En tout cas, pas au programme en S. Du moins, d'après mes souvenirs.
En prépa, oui par contre, bien qu'il nous soit quasiment 'interdit' de l'utiliser puisque d'autres théorèmes sont aussi simples et bien plus puissants.
-
kiosquamuffins
- Membre Naturel
- Messages: 13
- Enregistré le: 27 Jan 2012, 19:10
-
 par kiosquamuffins » 30 Jan 2012, 20:47
par kiosquamuffins » 30 Jan 2012, 20:47
Dante0 a écrit:Pas vraiment. On tombe sur une forme indéterminée en gros puisque le haut et le bas tendent vers +oo
Je peux pas utiliser le théorème de l'hopital ici ?
En principe tu as du voir cela en cours. Mais je veux bien te refaire la démo. Connais tu la limite de exp(x)/x ?
-
mathelot
 par mathelot » 31 Jan 2012, 05:21
par mathelot » 31 Jan 2012, 05:21
Bonjour,
}{x}=0) démonstration
démonstrationLa courbe du logarithme népérien est sous sa droite tangente
)
en
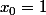
car la fonction est concave , de dérivée seconde

en faisant
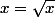
 \leq \sqrt{x}+1)
 \leq 2 \left( \sqrt{x}+1 \right))
}{x} \leq 2 \left(\frac{1}{ \sqrt{x}}+\frac{1}{x} \right))
donc
}{x}=0)
en faisant
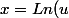)
qui est positif pour
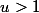
, on trouve le résultat demandé.
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 31 Jan 2012, 10:11
par el niala » 31 Jan 2012, 10:11
concavité et dérivée seconde c'est au programme de TS ? il me semblait que ce type d'exercice se traitait par croissance comparée des fonctions expo et identité (ou identité et log)
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 31 Jan 2012, 10:20
par sad13 » 31 Jan 2012, 10:20
Oui, on le démontre avec les croissances comparées en terminale.
La concavité, en enseignement supérieur certains l'ignorent que dire en TS
-
mathelot
 par mathelot » 31 Jan 2012, 12:50
par mathelot » 31 Jan 2012, 12:50
bah, "concave" est une explication suffisante pour
 \leq x+1)
inégalité que l'on peut démontrer en dressant un tableau de variations sans en comprendre
les tenants et aboutissements
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 31 Jan 2012, 16:11
par sad13 » 31 Jan 2012, 16:11
Mathelot, ce n'est pas plutôt ln(x)<=x-1 car la tangente en 1 est d'équation y = f'(1)*(x-1)+f(1)=x-1
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Fév 2012, 18:52
par Dante0 » 01 Fév 2012, 18:52
mathelot a écrit:bah, "concave" est une explication suffisante pour
 \leq x+1)
inégalité que l'on peut démontrer en dressant un tableau de variations sans en comprendre
les tenants et aboutissements
Euh quel rapport entre
 \leq x+1)
et la concavité ?
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 01 Fév 2012, 23:52
par sad13 » 01 Fév 2012, 23:52
Une fonction est concave <=> sa courbe est au dessous de ses tangentes et l'équation de la tangente en ......... est...........
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Fév 2012, 09:06
par Dante0 » 02 Fév 2012, 09:06
sad13 a écrit:Une fonction est concave sa courbe est au dessous de ses tangentes et l'équation de la tangente en ......... est...........
Je suis un peu perdu, la tangente de quelle fonction ? lnx ? Et en quel point ? Pourquoi ce serait 1 ? (cf ton dernier message)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Fév 2012, 09:21
par Sylviel » 02 Fév 2012, 09:21
Une des définitions de "fonction concave" c'est que son graphe est sous ses tangeantes. En particulier sous celle issue de 1 (mais aussi vrai pour les autres), et de là tu déduis l'inégalité nécessaire. Cependant cette caractérisation est hors programme. Une étude de signe sur la fonction x-1-ln(x) suffit à prouver l'inégalité voulue avec les outils basique de Tale.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Fév 2012, 14:44
par Dante0 » 03 Fév 2012, 14:44
Sylviel a écrit:Une des définitions de "fonction concave" c'est que son graphe est sous ses tangeantes. En particulier sous celle issue de 1 (mais aussi vrai pour les autres), et de là tu déduis l'inégalité nécessaire. Cependant cette caractérisation est hors programme. Une étude de signe sur la fonction x-1-ln(x) suffit à prouver l'inégalité voulue avec les outils basique de Tale.
Ok merci ! Mais je ne comprends pas le lien avec ma limite ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 07 Fév 2012, 15:33
par Dante0 » 07 Fév 2012, 15:33
Un petit up
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 07 Fév 2012, 16:24
par sad13 » 07 Fév 2012, 16:24
Dan sla démo de ta limite, on utilisait l'inégalité : lnx<=x-1 et cela est obtenu(entre autres) par la concavité du ln; cela dit, c'est aps trop au niveau Term et comme te l'a souligné Sylviel, c'est facilement faisable avec une étude de al fonction g(x)=lnx-(x-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
quand x tend vers +oo ?