[Discussion Terminée] Les nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 16:06
par haricot29 » 18 Oct 2006, 16:06
Coucou, je vais avoir besoin d'un peu d'aide pour des exos en maths =/ parce que je n'y arrives pas trop... Alors je mets l'énoncé, je les cherchent et dés que j 'ai quelques choses a vous proposez je le mets comme cela vs pourrez me dire si c'est ok !!! Merci d'avance, si vs avez des propositions pour que j'arrive mon exo je prends tout !
HaRiCoT_29
exercice 1 :id:
soit


(pi/2) [pi], déterminer le module et l'argument de z= 1+ cos 2;) + i*sin2;)
Merci d'avance !!!!!!!!!
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 16:08
par haricot29 » 18 Oct 2006, 16:08
exercice 1
z= 1+cos2;) +i*sin2;)
cos2;) = 2cos²;) -1 et sin2;) = sin;) *cos;) dc
z= 2cos²;) + 2*i*sin;)*cos;)
z= 2cos;) (cos;) + i*sin;)) --> forme trigo
module de z = 2cos;)
C'est ok ça ?!
si z=a+ib
pour cos;) = a/ module de z
pour sin;) = b/ module de z
mais ça bug !
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 18 Oct 2006, 16:49
par fonfon » 18 Oct 2006, 16:49
salut,
haricot29 a écrit:exercice 1
z= 1+cos2;) +i*sin2;)
cos2;) = 2cos²;) -1 et sin2;) = sin;) *cos;) dc
z= 2cos²;) + 2*i*sin;)*cos;)
z= 2cos;) (cos;) + i*sin;)) --> forme trigo
module de z = 2cos;)
C'est ok ça ?!
oui c'est ok mais moi je fais comme ça c'est plus joli
on a
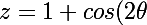+isin(2\theta))
or
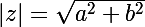
avec a=Re(z) et b=I(z)
donc
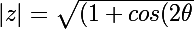)^2+(sin(2\theta))^2})
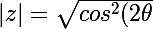+2cos(2\theta)+1+sin^2(2\theta)})
or
}+sin^2(\theta)=1)
donc
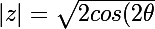+2})
donc
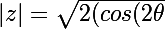+1)}=\sqrt{(4cos^2(\theta)})
essaie de poursuivre
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 19:11
par haricot29 » 18 Oct 2006, 19:11
z= racine (2 (2cos²;)-1 +1))
=racine (2*2cos²;))
= racine (4cos²;) )
= 2cos;) ??????????
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 19:22
par haricot29 » 18 Oct 2006, 19:22
euh mouais c'est bon ça ? bizar non ? :dingue2:
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 19:38
par haricot29 » 18 Oct 2006, 19:38
Y pas quelqu'un pour me filer un ti coup de pouce please ! :triste:
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 20:03
par haricot29 » 18 Oct 2006, 20:03
SVP ! :triste: :doh:
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 18 Oct 2006, 20:50
par haricot29 » 18 Oct 2006, 20:50
:hum: bon ben je laisse tomber pour ce soir je n'y arrives po !!!!
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 19 Oct 2006, 08:08
par fonfon » 19 Oct 2006, 08:08
pour le module tu as trouvé une simplification car:
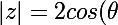)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 19 Oct 2006, 08:36
par fonfon » 19 Oct 2006, 08:36
Bonjour,
on a
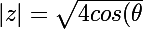}=|2cos(\theta)|)
il faut etudier selon le signe de cos
donc 2 cas à traite si

alors cos est ....
si

alors cos est ...
-
haricot29
- Membre Rationnel
- Messages: 612
- Enregistré le: 30 Oct 2005, 17:55
-
 par haricot29 » 19 Oct 2006, 18:50
par haricot29 » 19 Oct 2006, 18:50
Ok merci bcp ! c'est bon j'ai fini mon exo 1 j'ai reussi a trouver l'argument
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités