Les combinatoires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 21:28
par sousoushi » 06 Jan 2007, 21:28
bonjour je suis bloquée pr un exercice merci davance pr votre aide
^:puissance (n_1): 1 parmis n
1 .a. dvlopper f(x)=(1+x)^n
b. en deduire que pr tt reel x on a
n(1+x)^(n-1)= (n_1)+2(n_2)x +3(n_3)x^2+...+n(n_n)x^(n-1)
2. calculer
(n_1) + 2(n_2) + 3(3_n)+ ...+ n(n_n)
pour la 1.a/ je developpe avec la formule du binome sa me fait:
f(x)= (n_0)1^n + (n_1)1^(n-1) x +(n_2)1^(n-2) x²+...+(n_(n-1))1x^(n-1) + (n_n)x^n
aprés je ne vois pas comment en deduire la suite
et pour la 2eme question je ne trouve pas la methode pour faire le calcul
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 21:35
par amine801 » 06 Jan 2007, 21:35
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 21:39
par sousoushi » 06 Jan 2007, 21:39
la formule du binome de newton pour faier la deduction?? ou le calcul en 2
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 21:42
par amine801 » 06 Jan 2007, 21:42
sousoushi a écrit:la formule du binome de newton pour faier la deduction?? ou le calcul en 2
???
pour calculer la a :id: ensuite utilise la formule obtenue pour
deduire la b
excuse j'avais la flem de tout lire
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 21:45
par sousoushi » 06 Jan 2007, 21:45
mais jai deja calculer la a faut juste developpé !!
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 21:46
par sousoushi » 06 Jan 2007, 21:46
en faite le probleme c que je ne vois pa comment en deduire la b
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 21:54
par sousoushi » 06 Jan 2007, 21:54
f(x)= (n_0)1^n + (n_1)1^(n-1) x +(n_2)1^(n-2) x²+...+(n_(n-1))1x^(n-1) + (n_n)x^n
jai remplacé n par n-1 mais por trouver le b/ il faut aussi multiplié par n et quand je fait le calcul je ne trouve pas la meme chose :mur:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 21:57
par amine801 » 06 Jan 2007, 21:57
resonne en utilisan la derive remarque que
la derive de f est n(1+x)^(n-1)
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 22:00
par sousoushi » 06 Jan 2007, 22:00
sachant que c la derive en quoi sa peut expliquer le b/ ??
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 22:03
par amine801 » 06 Jan 2007, 22:03
t'as trouve
f(x)= (n_0)1^n + (n_1)1^(n-1) x +(n_2)1^(n-2) x²+...+(n_(n-1))1x^(n-1) + (n_n)x^n
donc
f'(x)=n(1+x)^(n-1)=[ (n_0)1^n + (n_1)1^(n-1) x +(n_2)1^(n-2) x²+...+(n_(n-1))1x^(n-1) + (n_n)x^n]'
je te laisse faire le calcule
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 22:12
par sousoushi » 06 Jan 2007, 22:12
d'accord mais comment tu faire pour derivé sa :(n_1)1^(n-1) x par exemple ?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 22:17
par amine801 » 06 Jan 2007, 22:17
on veut derive
 }.x)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 22:21
par amine801 » 06 Jan 2007, 22:21
on veut derive
 }.x)
cette expression est equivalent a cela
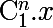
donc on derive paraport a x la valeur de n n'est pas importante
on obtient ainsi
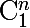
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 22:21
par sousoushi » 06 Jan 2007, 22:21
je ne connais pas la formule de la dérivé ...
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 22:26
par sousoushi » 06 Jan 2007, 22:26
jai fais les calculs mais je ne trouve pas sa:
(n_1)+2(n_2)x +3(n_3)x^2+...+n(n_n)x^(n-1)
en faite il manque le 2 devant (n_2) le et 3 devant (n_3).......
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 22:41
par amine801 » 06 Jan 2007, 22:41
sousoushi a écrit:d'accord mais comment tu faire pour derivé sa

n_1)1^(n-1) x par exemple ?
ce cas est un peut trop particulier miss dans le ca par exmple
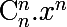
donc on derive paraport a x la valeur de n n'est pas importante
on obtient ainsi
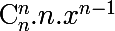
ps:
si
=u^n)
alors
=n.u'.u^n-1)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 22:53
par amine801 » 06 Jan 2007, 22:53
jete un coup d'oeuil au message car je l'est modifie
-
sousoushi
- Membre Naturel
- Messages: 77
- Enregistré le: 06 Jan 2007, 21:18
-
 par sousoushi » 06 Jan 2007, 23:02
par sousoushi » 06 Jan 2007, 23:02
ok mais en faite je ne pense pas que ce soit la méthode que je dois utilisé c'est tro compliqué sinon c moi qui n'arrive pas a bien faire la dérivé
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 23:09
par amine801 » 06 Jan 2007, 23:09
je pense qu'il faut que tu revise ton cours de derives :livre: :livre: :livre: :livre:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 06 Jan 2007, 23:11
par amine801 » 06 Jan 2007, 23:11
et pour la 2 ca va
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
