Les Branches de probabilités

[AMARI]

Bonjour à Tous,

Les données :
2 Urnes, U1 et U2.
U1 : 5 Boules rouges numérotées ( 0,1,1,1,2) + 3 Boules vertes numérotées (0,1,1).
On tire 2 Boules sans remise.
U2 : 3 Boules rouges numérotées (1,1,2) + 2 Boules vertes numérotées (0,1).
On tire 2 Boules avec remise.
"A": Les 2 Boules sont de même couleur.
"B": Les 2 Boules ont le même N°.
Questions :
Sachant que les 2 Boules sont de couleurs différentes, qu'elle est la probabilité qu'elles soient de l'urne U1?
J'ai essayé les branches suivantes:
"A": Les 2 Boules sont de même couleur.
"B": Les 2 Boules ont le même N°.
"C": Les 2 Boules ont le même N° et la même couleurs.
"D": Les 2 Boules ont le même N° et différentes couleurs.
"E": Les 2 Boules ont la même couleur et différents N°
"F": Les 2 Boules ont différentes couleurs et différents N°.
Tous ces cas existent et quels sont les cas à prendre ?
Je n'arrive pas à obtenir le chiffre "1" aux 2 Nœuds de U1 et U2.

Je vous Remercie vivement.

[catamat]

Bonjour

Je suppose (parce que ce n'est pas précisé dans ton message) que l'on choisit une urne au hasard puis on tire deux boules dans l'urne choisie.

Ici les numéros ne sont pas considérés on s'intéresse seulement à la couleur.

Les événements à considérer sont U1= "on choisit U1", U2= "on choisit U2" puis et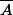
On demande
c'est à dire
avec
...
Est ce que cela suffit pour te permettre de terminer ?

[catamat]

On a aussi


avec qui est la proba de tirer deux boutes de couleur différentes de l'urne U1, donc facile à calculer.

[AMARI]

Bonjour catamat,

Oui j'ai oublié de mentionner qu'on choisit une urne au hasard puis on tire deux boules dans l'urne choisie.
Mais on nous demande aussi, est-ce que les événements "A" et "B" sont indépendants ?
Donc, il faut introduire l'évènement "B" dans les calculs pour voir si :
P(A(inter)B) = P(A) x P(B) (indépendants ou pas).

Merci catamat

[catamat]

Ok
Ma fois on procède de la même façon pour calculer P(A) ou alors puisqu'on vient de calculer on en déduit p(A)

pour p(B) idem

et enfin pour

Bon quand on choisit dans U2 pour avoir deux boules de même couleur et de même numéro c'est un peu plus compliqué car ce sont des tirages avec remise donc par ex on peut avoir deux fois la verte n°0, soit un cas favorable ou deux fois une rouge n°1, il y en a deux donc cela fait 2*2 cas favorables etc....

[AMARI]

Bonjour catamat,

Pour ce dernier cas compliqué dans (U2), est-ce qu'on peut écrire que pour la même couleur et le même N° que :
P(A∩B)∩(U2) = (2²+ 1² + 1² + 1²)/(5²) = 7/25.

Un Grand Merci catamat.

[catamat]

Ton calcul correspond à il faut ensuite le multiplier par p(U2) soit 1/2 (si le choix des urnes est équiprobable).

[AMARI]

Bonjour et Merci Beaucoup catamat pour tout ce calcul.

Bonne Journée