TS : Intro à la fonction exponentielle

par **magnum13** » 15 Sep 2009, 17:16

Bonjour, Voila mon exercices

Exercice 2 :

f est la fonction définie sur R par f(x) = x e^-x

Démontrer par récurrence que pour tout entier n>0, la dérivée n-ième de f est f^(n) (x) = (-1)^n * (x-n) * e^-x

J'avais deux autres exercices que j'ai déjà fait mais celui là je n'y arrive pas du tout, si vous pouviez m'aider pour débuter.

Merci

par **girdav** » 15 Sep 2009, 17:24

Bonjour.
Tu as fait l'initialisation?
Sinon pour l'hérédité ça découle de la formule de dérivation d'un produit.

par **magnum13** » 15 Sep 2009, 17:34

girdav a écrit:Bonjour.
Tu as fait l'initialisation?
Sinon pour l'hérédité ça découle de la formule de dérivation d'un produit.

L'initialisation ?

Je n'est pas compris comment fonctionne la démonstration par récurrence.

Merci

par **girdav** » 15 Sep 2009, 17:38

En fait tu as une proposition

qui dépend de

et tu veux montrer qu'elle est vraie pour

.
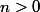
Le raisonnement par récurrence consiste à montrer que:
- la propriété est vraie au rang initial
- pour

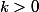
quelconque, si on a

alors on doit avoir

par **magnum13** » 15 Sep 2009, 17:42

ok mais comment puis-je commencer ma démonstration ?

Merci

par **girdav** » 15 Sep 2009, 17:48

On a que

est la proposition

.
Il faut montrer dans un premier temps que

est vrai.
Puis, suppose que

. Que vaut

?

par **magnum13** » 15 Sep 2009, 19:26

girdav a écrit:On a que est la proposition .
Il faut montrer dans un premier temps que est vrai.
Puis, suppose que . Que vaut ?

Je ne vois pas comment prouver que

est vrai.

par **girdav** » 15 Sep 2009, 19:27

Calcule

et montre que ça vaut

.

par **magnum13** » 15 Sep 2009, 20:32

girdav a écrit:Calcule et montre que ça vaut .

f'(x) =

+ x *

* -1
=

- x *

par **girdav** » 15 Sep 2009, 20:37

Ok, tu peux donc passer à la deuxième étape.

par **magnum13** » 15 Sep 2009, 20:47

girdav a écrit:Ok, tu peux donc passer à la deuxième étape.

par **girdav** » 15 Sep 2009, 21:01

Je crois qu'il y a une erreur de parenthèses. Tu peux montrer les détails de ton calcul de la dérivée de

?

par **magnum13** » 16 Sep 2009, 11:43

Je ne comprends plus, pourrai tu me dire les étapes à faire pour arriver à démontrer, merci beaucoup.

par **girdav** » 16 Sep 2009, 11:55

Tu dérives

: c'est le produit de deux fonctions, avec une constante devant.

par **magnum13** » 16 Sep 2009, 14:28

par **magnum13** » 16 Sep 2009, 17:03

S'il vous plait !!

par **girdav** » 16 Sep 2009, 17:51

Mets

en facteur.

par **magnum13** » 16 Sep 2009, 17:55

girdav a écrit:Mets en facteur.

Mais j'ai qu'un

et un

par **girdav** » 16 Sep 2009, 18:06

Ca devrait être un

. Il sort d'où sinon?

par **magnum13** » 16 Sep 2009, 18:20

TS : Intro à la fonction exponentielle

TS : Intro à la fonction exponentielle

Qui est en ligne