Intégration

par **Nisrina** » 29 Mar 2007, 08:04

Bonjour ,

soient :

et

je cherche

en fonction de

et

.
en fait , je trouve une relation entre

et

mais j'arrive pas à introduire

.

merci !

par **Flodelarab** » 29 Mar 2007, 10:29

A priori, une intégration par partie de Jn fait l'affaire.
Qu'est ce qui t'oblige à utiliser In ?

par **titine** » 29 Mar 2007, 10:50

Es tu bien sûr de ton énoncé ?
C'est bizare car Jn est calculable ...

par **Nisrina** » 30 Mar 2007, 01:16

bonsoir,

Flodelarab , j'y arrive pas :triste: j'ai tenté toutes les ipp possibles mais je ne trouve plus cette relation et même la relation que j'ai trouvé entre

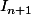
et

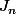
je crois qu'elle fausse car aprés on me demande de montrer que :

,et c pas ça ce que je trouve.
en effet titine , c vrai que

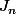
est calculable (je trouve

) mais c'est pas ça l'intérêt de l'exo il me semble .

voilà l'intégralité de mon exo :
1) calculer

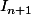
en fct de

et

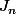
2) m.q :

3) en déduire

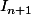
en fct de

4) mq:

5) mq:

6) posons :

calculer

- m.q :

-calculer

7) calculer la limite de

.

bon voilà , j'ai besoin juste de qq indication pour la début et j'essaierai le reste .

merci !

par **Blueberry** » 30 Mar 2007, 05:35

Bonjour,

En intégrant par partie mais en prenant t-1 comme primitive de 1 (et pas t) on arrive à faire apparaître Jn. J'obtiens la relation :

In+1 = 1 -2(n+1)In+1 +2(n+1)In -2(n+1)Jn

d'où : (2n+3)In+1 = 1 + 2(n+1)(In-Jn)

par **titine** » 30 Mar 2007, 06:58

Ouais ! Bravo Blueberry !
Mais franchement il est un peu tordu cet exo !

Attention Nisrina Jn = +1/(2(n+1))

Et alors après on ne trouve pas : In+1 = (2n+1)In mais In+1 = (2n+2)/(2n+3) In.
Résultat que j'avais trouvé directement sans utiliser Jn. Et ce résultat est confirmé par le calcul de I0 et I1. Donc l'énoncé est faux .

par **titine** » 31 Mar 2007, 07:59

Nisrina peux tu nous dire si tu as eu des précisions concernant ton exo car il y visiblement un problème.
Merci de nous tenir au courant.

par **sue** » 31 Mar 2007, 09:54

Bonjour,

désolée pour le retard , je viens de voir vos message .
merci Blueberry , mais j'aimerais savoir d'ou tu es parti pour l'intégration par partie , de

ou

dsl titine , j'ai fais une erreur de frappe , la question c mq :

, sinon la 3ème question n'aura aucun sens !

par **Nisrina** » 31 Mar 2007, 10:00

Bonjour ,

dsl pour le retard , je viens de voir vos messages .

merci Blueberry , mais j'aimerais savoir d'ou tu es parti(e) pour l'ipp , de

ou bien

?

dsl titine j'ai fais une erreur de frappe c :

, sinon la 3ème question n'aura aucun sens !

par **Blueberry** » 31 Mar 2007, 10:06

Bonjour Nisrina,

je suis parti tout naturellement de In+1 et j'ai fait l'ipp en primitivant 1 par t-1 comme je l'ai précisé.

par **titine** » 31 Mar 2007, 10:19

Comme le dit Blueberry il suffit d'intégrer par partie In+1 en posant :
u(x) = (1-t²)^(n+1) et v'(x) = 1
Mais en prenant v(x) = t-1

Mais je maintiens que je trouve cet exo tordu car à partir de là on trouve directement la relation entre In+1 et In puisqu'on sait calculer Jn ...

par **Blueberry** » 31 Mar 2007, 10:25

Bonjour titine,

en fait, comme déjà dit, Jn peut être calculé explicitement et on dirait que l'auteur de l'énoncé a commis une étourderie en intégrant par partie In+1, il semble avoir oublié de faire sortir le ''t'' provenant de la dérivée de t^2 si bien qu'il donne la relation inexacte à mon avis : In+1 = 2(n+1)Jn.

Ne penses tu pas que cette relation est fausse ?

par **Nisrina** » 31 Mar 2007, 10:26

je suppose qu'il faut faire une double ipp , car aprés on obtient :

et aprés je ne trouve qu'une relation ente

et

(en primitivant

) :hein:

par **Nisrina** » 31 Mar 2007, 10:32

Blueberry a écrit:si bien qu'il donne la relation inexacte à mon avis : In+1 = 2(n+1)Jn.

la relation demandée c'est :

par **Blueberry** » 31 Mar 2007, 10:35

Oui exact, ta relation est la bonne mais si tu réintègre par partie cette intégrale tu retombes sur In+1 qui disparaît de la relation puisqu'on l'a des deux côtés de l'égalité. Finalement on retrouve encore Jn = 1/2(n+1) !

par **Nisrina** » 31 Mar 2007, 10:45

oui c'est ce que je trouve !

je désespère ... :mur:

par **Nisrina** » 31 Mar 2007, 10:48

titine a écrit:Et alors après on ne trouve pas : In+1 = (2n+1)In mais In+1 = (2n+2)/(2n+3) In.
Résultat que j'avais trouvé directement sans utiliser Jn. Et ce résultat est confirmé par le calcul de I0 et I1. Donc l'énoncé est faux .

comment tu as fais titine sans utiliser

?

par **titine** » 31 Mar 2007, 11:05

Nisrina a écrit:comment tu as fais titine sans utiliser ?

Si, si, justement j'ai utilisé Jn = +1/(2(n+1)) !!

par **Blueberry** » 31 Mar 2007, 11:13

On peut aussi l'obtenir en intégrant une fois par partie en primitivant 1 par t.

par **titine** » 31 Mar 2007, 11:14

Oui, oui, exact ! Excuse moi !

Intégration

intégration

Qui est en ligne