Integration par décomposition en fraction partielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anime4ever
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Avr 2008, 02:37
-
 par anime4ever » 08 Avr 2010, 22:48
par anime4ever » 08 Avr 2010, 22:48
Bonjour,
j'ai de la difficulté avec certaines intégrales.
La premiere est
^3} dx)
Est ce que pour la résoudre je dois la mettre comme ceci;
^2}+ \frac{D}{(2x+3)^3})
????
Ou 3 fois sans les exposant au dénominateur?
Oui je me suis forcé pour écrire en TEX, oufff.
Merci.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 08 Avr 2010, 23:32
par Hiphigenie » 08 Avr 2010, 23:32
Bonsoir,
Heureusement ou malheureusement, tu as raison. C'est bien comme tu le dis qu'il faut transformer l'énoncé...
^2} + \frac{D}{(2x+3)^3)
-
anime4ever
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Avr 2008, 02:37
-
 par anime4ever » 08 Avr 2010, 23:46
par anime4ever » 08 Avr 2010, 23:46
Mais dans le solutionnaire il m'indique qu' une fois décomposé (pas intégré) c'est;
^3})
Ce n'est pas normal puisque quand il y a un exposant de puissance 3 il faut le faire trois fois non?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 09 Avr 2010, 00:09
par Hiphigenie » 09 Avr 2010, 00:09
Oui, mais si B et C sont nuls...
As-tu essayé la décomposition ?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 09 Avr 2010, 00:19
par Hiphigenie » 09 Avr 2010, 00:19
Et c'est le cas !
^3}=\frac{A}{x} +\frac{B}{2x+3}+\frac{C}{(2x+3)^2}+\frac{D}{(2x+3)^3})
^3}=\frac{A(2x+3)^3 +Bx(2x+3)^2 + Cx(2x+3) + Dx}{x(2x+3)^3})
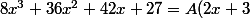^3 +Bx(2x+3)^2 + Cx(2x+3) + Dx)
Posons x = 0, alors : 27 = 27A, soit A = 1
Posons
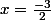
, alors
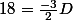
, soit D = -12.
Posons x = -1, alors : 13 = A - B - C - D, soit 13 = 1 - B - C + 12 ou 13 = 13 - B - C ou B + C = 0
Posons x = -2, alors : 23 = -A - 2B + 2C - 2D, soit 23 = -1 - 2B +2C + 24 ou 23 = 23 - 2B +2 C ou B - C = 0
Les système
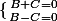
admet comme solution : B = 0 et C = 0
Par conséquent :
^3}=\frac{1}{x} -\frac{12}{(2x+3)^3})
-
anime4ever
- Membre Naturel
- Messages: 18
- Enregistré le: 02 Avr 2008, 02:37
-
 par anime4ever » 09 Avr 2010, 01:04
par anime4ever » 09 Avr 2010, 01:04
Je dois te remercier pour tout ton aide. Tu as pris une bonne heure pour m'écrire une démarche détaillé qui m'a aidé a comprendre.
Merci beaucoup
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 09 Avr 2010, 06:48
par Euler07 » 09 Avr 2010, 06:48
Programme de fac ça !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités