Khôlle : dérivabilité et intégration

par **Nightmare** » 12 Mar 2010, 17:04

Salut :happy3:

L'ayant déjà préparée, je poste l'unique exo de khôlle pour la semaine prochaine, pour ceux que ça intéresse. Il s'agit d'un exo en trois parties.

Approximation quadratique :

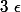
I] Rappel de cours : Démontrer que f est dérivable en 0 si et seulement s'il existe une fonction qui tend vers 0 en 0 telle que .

II]Au delà de l'approximation affine :
f est une fonction deux fois dérivables (principalement au voisinage de 0) et dont la dérivée seconde est continue.

. .1) En intégrant par parties, calculer pour x quelconque.

. .2)* Montrer que
(on pourra écrire que )

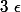
. .3) Déduire de 1) et 2) que où est une fonction qui tend vers 0 en 0.

III] Applications et contre-exemple

. .1) Calculer

. .2)* Trouver une fonction f telle qu'il existe a,b et c tels que avec mais qui ne soit pas deux fois dérivables en 0.

Amusez-vous bien :happy3:

P-S : La khôlle de la semaine prochaine dure spécialement 1h30, d'où l'exercice un peu long :lol3:

par **benekire2** » 12 Mar 2010, 17:38

merci !! Je le ferais ce we !! :zen:

par **Nightmare** » 13 Mar 2010, 13:40

Pour les élèves les plus talentueux, j'attends une généralisation du résultat du II] :lol2:

par **benekire2** » 13 Mar 2010, 13:53

A vue de nez ça ressemble fort aux formules de Taylor

par **Nightmare** » 13 Mar 2010, 13:57

Ben oui, en II] on forme un DL d'ordre 2, le but de l'exercice est donc de le justifier.

par **benekire2** » 13 Mar 2010, 13:59

Voui voui :id:

J'ai pas eu le temps de le faire encore, j'ai les oraux des TPE a préparer... on a fait sur le nombre d'or :zen: et j'ai pris toute la partie math ( sinon j'aurais rien fait je crois :marteau: )

par **Nightmare** » 13 Mar 2010, 14:13

Seule les questions étoilées prennent du temps normalement :happy3:

par **benekire2** » 13 Mar 2010, 16:37

Nightmare a écrit:Seule les questions étoilées prennent du temps normalement :happy3:

Oui mais j'en ai fais aucune pour le moment ^^

par **benekire2** » 13 Mar 2010, 18:24

Pour la 2 du II
ton indice on fait comment pour l'utiliser, parce que comme on a calculé l'intégrale juste avant, je n'ai plus de f'' mais plus que des f et des f' ?

par **Nightmare** » 13 Mar 2010, 18:27

La résolution de la 2) ne dépend pas du résultat obtenue en 1) !

par **benekire2** » 13 Mar 2010, 18:28

Nightmare a écrit:La résolution de la 2) ne dépend pas du résultat obtenue en 1) !

Ok ok :zen:

par **Nightmare** » 13 Mar 2010, 18:39

Pour la 2), la continuité de la dérivée seconde joue un rôle.

par **benekire2** » 13 Mar 2010, 18:41

Et bien je dois te dire, que je n'arrive pas a faire la II-2 la II-3 et la III-2 :ptdr:
Par ou commencé dans la II - 2 ??

par **Nightmare** » 13 Mar 2010, 18:45

Eh bien, commencer par utiliser l'indice :lol3:

Je commence pour te mettre sur la voie :

Essaye de calculer la première et déduis-en ce que tu dois prouver pour la deuxième, et prouve le :lol3:

par **benekire2** » 13 Mar 2010, 18:56

Je trouve x²/2 pour la première, donc si je sépare la fraction, je pense qu'on devrait trouver :

(Intégrale restante)/x²= 1/2 f''(0)-1/2

C'est ça ?

par **benekire2** » 13 Mar 2010, 19:07

Pour la premièreon trouve bien :

xf'(0)-f(x)+f(0) ?

par **Nightmare** » 13 Mar 2010, 19:10

benekire2 a écrit:Je trouve x²/2 pour la première, donc si je sépare la fraction, je pense qu'on devrait trouver :

(Intégrale restante)/x²= 1/2 f''(0)-1/2

C'est ça ?

x²f''(0)/2 plutôt pour la première non?

Sinon pour continuer cette question, n'oublie pas qu'on calcule une limite !

Ton résultat du I] est juste.

par **benekire2** » 13 Mar 2010, 19:35

Nightmare a écrit:x²f''(0)/2 plutôt pour la première non?

Sinon pour continuer cette question, n'oublie pas qu'on calcule une limite !

Ton résultat du I] est juste.

A ba voui, j'avais foirer le calcul.

Donc

( Edit il faut lire avec des doubles primes et non des simples ... )

doit tendre vers 0 en principe. Mais comment savoir quelle doit être la valeur de l'intégrale ?

Bref, aujourd'hui je fais que de la grosse m.. j'arrive rien a faire :triste:

par **Nightmare** » 14 Mar 2010, 01:42

Attention, ce sont des f'' et non des f' !

Vue que la première intégrale vaut x²/2f''(0), il faut montrer que ton truc tend vers 0. Pour cela je t'ai dit, utilise le fait que la fonction est continue sur le segment [0,x]

par **benekire2** » 14 Mar 2010, 08:26

ce sont bien des f'' mais c'est que ça a mal passé au latex !! ( j'avais précisé juste au dessus :we: )

Khôlle : dérivabilité et intégration

khôlle : dérivabilité et intégration

Qui est en ligne