bonjour à tous voilà j'ai ce petite exercice a finir pour aujourd'hui mais je n'y comprend rien! :hein:
pourriez_vous m'aidez à le résoudre
1) A partir de l'encadrement -1<=cos t<=1 valable pour tout t
montrer que pr tout x>=0; -x<=sin x<=x
2) Justifier qu'il en découle, pour tout x>=0
(-1/2)x²<=1-cosx<=1/2x², puis x-(1/6)x^3<=sinx<=x
Merci pour votre aide! :triste:
Integration
8 messages
- Page 1 sur 1
pour la second unitile d'élèves au carré
 \leq x)
alors
dx \leq \int x dx)
+cte \leq \frac{x^2}{2})
pour une valeur de 0 on a

alors
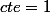
donc
\leq \frac{x^2}{2})
------------------------------------------------------------------------
alors en marche pour la 3
donc on a
\leq \frac{x^2}{2})
alors
)dx\leq \int \frac{x^2}{2}dx)
+cte\leq \frac{x^3}{6})
en fesant la verification avec 0
on a cte=0
alors
\leq \frac{x^3}{6})
avec une inversion de singe on a (multiplie pas -1)
-x\leq \frac{x^3}{6})
alors
\leq \frac{x^3}{6}+x)
et on utilisan la reponse 1 on a alors
\leq x)
alors
pour une valeur de 0 on a
alors
donc
------------------------------------------------------------------------
alors en marche pour la 3
donc on a
alors
en fesant la verification avec 0
on a cte=0
alors
avec une inversion de singe on a (multiplie pas -1)
alors
et on utilisan la reponse 1 on a alors
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 119 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
