Integration

[mosin]

bonjour

pouvez vous m'aidez sur cet exo

ps si quelqu'un a un anabac il doit etre dedans

merci :we:

[fonfon]

Salut, tu bloques où?

[Nightmare]

Bonsoir

Tu pourrais faire l'effort de recopier ton énoncé ...

[Daragon geoffrey]

slt
pour la première calcule In+Un, tu es censé tombé sur 1/2, ainsi tu peux conclure. Ensuite pour comparer les 2 quotients redui o même denom. (ce qui est déjà fait et met en facteur t^n) la fraction obtenu est alor du signe du facteur entre parenthese : (t-1) or t est compris entre 0 et 1 équiv. à t-1 compris entre -1 et 0 donc négatif, alor on obtient t^(n+1)/(1+t) inf ou égal à t^n/(1+t) en intégrant (l'ordre étant conservé) tu obtients U(n+1) inf ou égal à Un équiv. à (Un) décroissante pour tt n de [0;1].
pour la trois de lamême manière étudie le signe de la différence (t^n/(1+t))-t^n on a : (-t^(n+1))/(1+t) qui est inf ou égal à 0 donc t^n/(1+t) inf ou égal à t^n, ces deux membres étant bien entendu (pour tt t positif ou nul) positif ou nul. si tu veux être vraiment rigoureux, pour montrer que t^n/(1+t) est positif ou nul étudie les variations de la fct associée ( mais ce n'est pas nécessaire) !
l'inégalité du 4 s'obtient en intégrant l'inégalité démontrée juste avant !
puis pour la dernière utilise le th des gendarmes, grâce à l'inégalité précédente tu conclu que lim Un=0.

[fonfon]

Salut, pour le 2) moi je dirais que:

pour tout t ds [0,1] on a t^n+10 donc


comme 0<1 , et donc


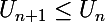
donc la suite (Un) est decroissante
A+

[fonfon]

Re, pour la 3) moi je procède comme pour la 2)

On a pour tout ds [0,1], et

et donc
On en deduit, comme 0<1, et donc on a :

4 d'après la question 3), on a pour tout t ds [0,1] et
on en deduit


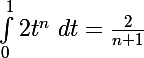
Or , donc on a bien:



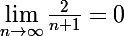
5) on a et donc par encadrement

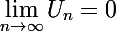
donc

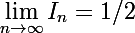
A+

[Mikou]

et 4,5 de gratuit au bac :happy: