Intégrale de Gauss

[upium666]

Bonjour à tous et à toutes
Je ne suis qu'en 1ère S et pourtant je m'attaque à cette fameuse intégrale
On se propose de calculer :



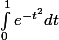
Sans démonstration (je ne le peux pas, j'ai cherché un peu sur internet :triste: ) je suis arrivé à ce résultat :



ou de manière plus simple :



1)Est-ce juste ?
2)Comment puis-je continuer pour arriver au calcul voulu ? (en valeurs exactes ! C'est à peu près 0.78 je pense mais je veux la valeur exacte)

Merci !

[skwouale]

le développement polynomial que tu écris correspond à la fonction d'erreur ERf(x), pour x = 1.

l'intégrale de exp(-t²) sur |R est égal à racine(Pi),
A part cela, la primitive de exp(-t²) n'est pas explicitable avec les fonction usuelles type exposants, polynomes, cos, sin etc...il faut juste faire le développement..

A+

[upium666]

le développement polynomial que tu écris correspond à la fonction d'erreur ERf(x), pour x = 1.

l'intégrale de exp(-t²) sur |R est égal à racine(Pi),
A part cela, la primitive de exp(-t²) n'est pas explicitable avec les fonction usuelles type exposants, polynomes, cos, sin etc...il faut juste faire le développement..

A+

Cela suggère que la réponse à mon 1) est "Oui" ? :p
Et comment puis-je faire pour obtenir la valeur exacte de ce développement ? :/

[Kikoo <3 Bieber]

C'est pas le plus simple !
Tout d'abord tu peux essayer de te documenter sur les intégrales doubles et une preuve via Fubini te sera accessible.
Sinon, une preuve encore plus accessible mais plus longue (niveau TS-maths sup) consiste à encadrer cette intégrale par des intégrales de Wallis et à faire tendre n vers l'infini.
Je te passerai l'énoncé pendant les vacances si tu veux.

[upium666]

C'est pas le plus simple !
Tout d'abord tu peux essayer de te documenter sur les intégrales doubles et une preuve via Fubini te sera accessible.
Sinon, une preuve encore plus accessible mais plus longue (niveau TS-maths sup) consiste à encadrer cette intégrale par des intégrales de Wallis et à faire tendre n vers l'infini.
Je te passerai l'énoncé pendant les vacances si tu veux.

Peut-être serait-il préférable de déplacer ce sujet dans le forum Supérieur ? :we: