Intégrale de Laplace-Gauss

[t.itou29]

Bonsoir,
Je bloque sur une question d'un exercice:
J'ai dû montrer que :


Ensuite il faut en déduire que:

Je suis arrivé à
Mais je ne vois pas quoi faire, la partie de gauche me fait penser à la définition de la limite en 0. Pouvez-vous me donner des pistes ? (pas la solution)
Merci

[t.itou29]

J'ai peut-être trouvé quelque chose : on a et , ce qui donne la définition de la limite en 0.
Mais j'ai dû me tromper puisque si , ne peut être <1. Il doit avoir une autre piste que de prendre la définition de la limite. Quelqu'un peut m'aider ?

[Fred_Sabonnères]

Est-ce qu'on peut écrire:



or

d'où le résultat :hein:

[t.itou29]

[quote="Fred_Sabonnères"]Est-ce qu'on peut écrire:

, je pense pas

[t.itou29]

Je suis arrivé à
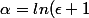En posant et on a donc

D'où
Si c'est bon, n'y aurait-il pas plus simple ?

[Archibald]

Bonsoir,

le terme "en déduire" impliquerait logiquement une démonstration utilisant l'encadrement donné auparavant, donc théorème des gendarmes ...

[t.itou29]

Bonsoir,

le terme "en déduire" impliquerait logiquement une démonstration utilisant l'encadrement donné auparavant, donc théorème des gendarmes ...

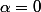
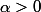
Oui c'est ce que je pensais. Mais pour que les deux cotés de l'encadrement soient égaux à 1 je dois prendre or ou alors je fais comme fred-sabonnères dit mais je sais pas si c'est bon comme il y a une limite où x tend vers 0 et les deux autres où alpha tend vers 0 ?
Comme on avait et ça m'a fait penser à la valeur absolue et donc à la définition formelle de la limite. C'est bon sinon ce que j'ai fait ?

[t.itou29]

Je me permets de faire remonter, j'ai réussi tout le problème et calculé l'intégrale de Laplace-Gauss mais il y a juste cette question qui me pose problème