Pour la première question :
-------------------------------------
(1):
 \in [0,+\infty[^2, (x \neq y) \Rightarrow (x - \frac{1}{sqrt{x}} \neq y - \frac{1}{sqrt{y}}))
Je vais essayer de prouver (1) par la
contraposée. En effet, Montrer (1) est équivalent à montrer que
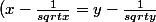 \Rightarrow (x = y))
A partir de là, on peut avoir l'idée d'introduire une fonction

définie par
=x-\frac{1}{sqrt x})
, et tenter de montrer que cette fonction est en fait
injective, c'est à dire que
=f(y))\Rightarrow (x=y))
.
Je remarque que
 \to - \infty)
quand
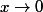
, et que
 \to +\infty)
quand
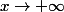
. Anecdotiquement, en a aussi
=0)
.

est donc "grosso modo" - macroscopiquement si on veut - croissante... L'idée qui me vient est alors d'essayer de montrer qu'elle est en réalité
strictement croissante. Pourquoi ? Parce que si cela marche,
de la stricte monotonie on pourra déduire l'injectivité, ce que je cherche à montrer.
Maintenant comment montrer que cette fonction est strictement croissante ? Bien entendu, on pense très vite à regarder du côté de la fonction dérivée : si elle est strictement positive, c'est gagné... Par contre je n'aime pas trop ce que va donner la dérivée de la fraction avec la racine carrée... donc je vais essayer de ruser un peu :
Après tout, si on pose
=x^2-\frac{1}{x})
et
=sqrt x)
, on a
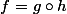
Je remarque que

est strictement croissante (c'est trivial), et que

aussi (calcule la dérivée de

, cela devient évident) :

est donc également strictement croissante en tant que composée de deux fonctions qui le sont.
De cette stricte monotonie, on déduit l'injectivité de

et donc ce qu'on cherchait à montrer.