Bonjour, Je vous sollicite pour pouvoir m'aider sur un dm de maths en ayant été absent.... Je vous joint l'énoncé et ce a quoi j'ai répondu !
Alors, Soit f la fonction définie par la relation f(x)=x²+x-1/x²+4x+5
1) Montrer que la fonction f est définie sur l'ensemble R, pour cela j'ai vu que c'était une fonction du type A/B et B doit être différent de 0 j'ai donc calculé son discriminant et j'ai trouvé -4 et comme -4<0 elle est définie sur R
Je vous préviens je bloque énormément après .....
2) Déterminer l'intervalle sur lequel la fonction f est dérivable puis calculer pour tout x de cet intervalle la dérivée f'(x).
pour déterminer son ensemble, je dois....
3) Résoudre l'équation f'(x)=0
4) Etudier le signe du polynôme 3x²+12x+9 sur l'intervalle ou f' est définie
5) étudier le signe du polynôme (x²+4x+5)² sur l'intervalle ou la dérivée f' est définie
6) en déduire le signe de la dérivée sur l'intervalle ou la dérivée f' est dérivée
7)en déduire le sens de variation de la fonction f sur son intervalle de définition
8) Calculer combien valent les minimums et les maximums s'il y'en a
9) Dresser le tableau de variation de la fonction f sur son intervalle de definition
10) Construire la représentation graphique Cf de la fonction sur l'intervalle [-10;10]
11) Déterminer les équations des tangentes a la courbe Cf en -3;-2;-1 et représenter ces tangentes sur le graphique.
Je sais que vous pensez que je vous demande juste pour que vous "fassiez" mon dm mais j'ai cherché pas mal de temps mais je n'y arrive pas c'est le seul dm de l'année ou je n'y arrive pas....
Alors si vous pourriez m'aider ce serait tres cool !
Cordialement Deadshot!
Help !! Pour un dm de maths en ayant été absent !
4 messages
- Page 1 sur 1
Re: Help !! Pour un dm de maths en ayant été absent !
Bonjour,
pour calculer ta dérivée, la fonction est de la forme u/v et sa dérivée est donc (u'v-v'u)/v².
A toi...
pour calculer ta dérivée, la fonction est de la forme u/v et sa dérivée est donc (u'v-v'u)/v².
A toi...
Re: Help !! Pour un dm de maths en ayant été absent !
bonjour,
la fonction f , ça ne serait pas
=\dfrac{x^2+x-1}{x^2+4x+5})
car quand tu l'as écrite, tu as dû oublier les parenthèses.
En effet, quand on l'écrit sans la présentation Latex (prononcer Latek),il faut parenthéser le numérateur et le dénominateur
Son domaine est bien car
car +1=(x+2)^2+1 \geq 1)
la fonction f , ça ne serait pas
car quand tu l'as écrite, tu as dû oublier les parenthèses.
En effet, quand on l'écrit sans la présentation Latex (prononcer Latek),il faut parenthéser le numérateur et le dénominateur
Son domaine est bien
Re: Help !! Pour un dm de maths en ayant été absent !
Salut !
2. Sais-tu ce qu'est le nombre dérivé, noté) , d'une fonction quelconque
, d'une fonction quelconque  définie sur un intervalle ouvert en un point d'abscisse
définie sur un intervalle ouvert en un point d'abscisse  ? C'est le coefficient directeur de la tangente
? C'est le coefficient directeur de la tangente 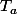 à la courbe représentative
à la courbe représentative  de
de  en
en  . La dérivée d'une fonction quelconque
. La dérivée d'une fonction quelconque  , notée
, notée  , est la fonction qui généralise le nombre dérivé de
, est la fonction qui généralise le nombre dérivé de  en un point quelconque.
en un point quelconque.
Si tu veux, grosso modo, une fonction est dérivable en un point si on peut tracer une tangente à la courbe en ce point.
Ici ta fonction est d'un type particulier : c'est une fonction dite rationnelle, c'est-à-dire une quotient de deux fonctions polynômes.
est d'un type particulier : c'est une fonction dite rationnelle, c'est-à-dire une quotient de deux fonctions polynômes.
--------------------------------------------------- Petite parenthèse ---------------------------------------------------
De manière générale, si= P(x)/Q(x)) , avec
, avec  et
et  deux polynômes et
deux polynômes et  un polynôme non constant,
un polynôme non constant,  sera définie pour tout réel
sera définie pour tout réel  tel que
tel que \ne 0) , donc sur
, donc sur ) , où
, où ) est l'ensemble des racines réelles de
est l'ensemble des racines réelles de  (c'est-à-dire l'ensemble des réels
(c'est-à-dire l'ensemble des réels  tel que
tel que =0) ). L'ensemble des racines
). L'ensemble des racines ) de
de  ne peut pas avoir plus de racine que le degré de
ne peut pas avoir plus de racine que le degré de  . Autrement dit, l'ensemble
. Autrement dit, l'ensemble ) est fini donc en fait
est fini donc en fait  sera une réunion d'intervalles ouverts (non réduits à un singleton). Soit
sera une réunion d'intervalles ouverts (non réduits à un singleton). Soit  un de ses intervalles ouverts ;
un de ses intervalles ouverts ;  est bien définie sur
est bien définie sur  donc dérivable sur
donc dérivable sur  .
.
---------------------------------------------------------------------------------------------------------------------------
Tout ça pour dire qu'en fait ici, est définie sur
est définie sur 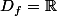 puisque tu as montrer que
puisque tu as montrer que =\emptyset) , où ici
, où ici =X^2+4X+5) n'a pas de racines réelles. Donc
n'a pas de racines réelles. Donc  est une fonction rationnelle définie un intervalle ouvert
est une fonction rationnelle définie un intervalle ouvert  donc
donc  est dérivable sur cet intervalle ouvert. L'idée (pas très rigoureuse) c'est qu'une fonction définie sur un intervalle ouvert par des fonctions de références "gentilles" est dérivable sur ce même intervalle ouvert. Mais il y a des exceptions, c'est pour ça que j'ai dit "gentilles". Par exemple la fonction racine carrée est définie sur
est dérivable sur cet intervalle ouvert. L'idée (pas très rigoureuse) c'est qu'une fonction définie sur un intervalle ouvert par des fonctions de références "gentilles" est dérivable sur ce même intervalle ouvert. Mais il y a des exceptions, c'est pour ça que j'ai dit "gentilles". Par exemple la fonction racine carrée est définie sur  alors qu'elle n'est dérivable que sur
alors qu'elle n'est dérivable que sur 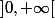 . La fonction valeur absolue est définie sur
. La fonction valeur absolue est définie sur  mais n'est dérivable que sur
mais n'est dérivable que sur  et sur
et sur 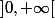 . Le mot ouvert pour l'intervalle sur lequel est définie la fonction est ici très important !
. Le mot ouvert pour l'intervalle sur lequel est définie la fonction est ici très important !
3. A l'aide de la formule donnant la dérivée d'un quotient de deux fonctions'= \frac{u'v-uv'}{v^2}) , montre que pour tout
, montre que pour tout  réel, tu as
réel, tu as = \frac{3x^2+12x+9}{(x^2+4x+5)^2}) .
.
4. et 5. te font étudier, suivant le réel , le signe du numérateur et du dénominateur de
, le signe du numérateur et du dénominateur de ) .
.
6. Découle de 4. et 5.
7. Là où \ge 0) ,
,  est croissante ; là où
est croissante ; là où  \le 0) ,
,  est décroissante. ("Là où" signifiant à quel ensemble appartient
est décroissante. ("Là où" signifiant à quel ensemble appartient  ).
).
8. Les éventuels minimum(s)/maximum(s) sont solutions de l'équation=0) , laquelle a été résolue à la question 3..
, laquelle a été résolue à la question 3..
9. Il s'agit de résumer dans un tableau ce qui a été trouvé aux questions précédentes.
11. C'est du cours : l'équation de la tangente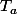 à
à  en
en  est
est 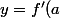 \times (x-a) +f(a)) .
.

2. Sais-tu ce qu'est le nombre dérivé, noté
Si tu veux, grosso modo, une fonction est dérivable en un point si on peut tracer une tangente à la courbe en ce point.
Ici ta fonction
--------------------------------------------------- Petite parenthèse ---------------------------------------------------
De manière générale, si
---------------------------------------------------------------------------------------------------------------------------
Tout ça pour dire qu'en fait ici,
3. A l'aide de la formule donnant la dérivée d'un quotient de deux fonctions
4. et 5. te font étudier, suivant le réel
6. Découle de 4. et 5.
7. Là où
8. Les éventuels minimum(s)/maximum(s) sont solutions de l'équation
9. Il s'agit de résumer dans un tableau ce qui a été trouvé aux questions précédentes.
11. C'est du cours : l'équation de la tangente
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
