Géométrie: triangles ...

[Anonyme]

Bonjour Bonjour
Mon professeur de Mathématique a donné qques exercices pour préparer le prochain DS etj 'ai beaucoup de mal donc voilà si qqun pourait m'indiquer la marche à suivre, enfin tout ce qu'il faut ça me serais vraiment utile parce qu'il ne faut vraiment pas que je loupe ce DS.
Donc voilà les exercices:


1er exercice:
ABC est un triangle équilatéral de côté 6cm. M est le point du côté [AB] tel que AM = 4cm.
La parallèle à (BC) passant par M coupe [AC] en D.
La parallèle à (AC° passant par M coupe [BC] en E.
1°)Démontrer que les triangles ABC, AMD et MBE sont de même forme.
2°)a)Démontrer que les triangles MAE et MDB sont isométriques.
b)Exprimer mes aires de AMD et MBE en fonction de l'aire de ABC.
c)Calculer l'aire du quadrilatère ADEB.



2eme exercice:Calculer un rapport de similitude
ABC est un triangle rectangle en A, [AH] est la hauteur issue de A.
K et L sont les symétriques de H respectivement par rapport aux droites (AB) et (AC).
a)En considérant des triangles isométriques, démontrer que A est le milieu de [KL].
b)Démontrer que les points A, H, B, K sont situés sur un même cercle. En déduire que : l'angle HKA = l'angle HBA.
c)Démontrer de même que : l'angle ALH = l'angle ACH
d)Démontrer que les triangles CAB et LHK sont de même forme. Etablir que le rapport de similitude du triangle ABC au triangle LHK est "k = (2AH)/BC".


3eme exercice: S'aider de la conclusion pour démontrer
Deux sécantes (AB) et (MN) à un cercle C de centre O et de rayon R, se coupent en un point P situé hors du cercle.
1°)On se propose de démontrer que :
PM x PN = PA x PB
a)Pour cela, écrire l'égalité à démontrer sous la forme PM/PA = ... ou PM/PB = ...
b)Déterminer alors des triangles de même forme dont les côtés interviennent dans les rapports du a)
c)En déduire l'égalité souaitée
2°)Exprimer le produit PM x PN en fonction de R et de la distance PO.


Voilà mon avenir est entre vos mains :) Merci

[Anonyme]

Voilà la figure pour le deuxième exercice:
http://img503.imageshack.us/img503/6613/photo1232hz.jpg

Et celle pour le 3eme exercice:
http://img503.imageshack.us/img503/6560/photo1228mp.jpg

[bernie]

Bonjour,

1°)Démontrer que les triangles ABC, AMD et MBE sont de même forme.

ABC et AMD d'abord :

angle A commun

angle AMD=^ABC (angles correspondants des 2 dr // (DM) et (BC) coupés par la sécante (AB)-->programme de 5e)

Ces 2 tr sont semblables car 2 angles égaux.

ABC et MBE :

angle B commun

angle MEB=^ACB(angles correspondants des 2 dr // (AC) et (ME) coupés par la sécante (BC))

Donc les 3 tr sont semblables (ou de même forme) donc AMD et MDE sont équi comme ABC.

2°)a)Démontrer que les triangles MAE et MDB sont isométriques.

MBE est équi donc MB=ME=6-4=2

AMD est équi donc MD=MA=4

angle AME=180-BME=180-60=120

angle DMB=180-DMA=180-60=120

Les 2 tr MAE et MDB ont un angle égal compris entre 2 côtés égaux donc ils sont isométriques.

b)Exprimer les aires de AMD et MBE en fonction de l'aire de ABC.

Les côtés de AMD et ABC sont sont ds le rapport 4/6=2/3 donc leur aire sont ds le rapport (2/3)²=4/9.

Les côtés de MBE et ABC sont sont ds le rapport 2/6=1/3 donc leur aire sont ds le rapport (1/3)²=1/9.

Je regarde la suite tout à l'heure si personne d'autre.

A+


c)Calculer l'aire du quadrilatère ADEB.

[bernie]

a)En considérant des triangles isométriques, démontrer que A est le milieu de [KL].

Soit M milieu de [HK] et N milieu de [HL]

On va montrer que LNA et AMK sont isom..

ANHM est un rectangle (3 angles droits).

AN=HM=MK

AM=NH=NL

Les 2 tr rect LNA et AMK sont iso...car ils ont 2 côtés égaux.

Donc AL=AK mais il faut montrer de plus que angle LAK=angle plat.

angle LAN est complémentaire d'angle ALN donc de KAM donc :

LAN+KAM=90° et LAN+KAM+NAM=180°

b)Démontrer que les points A, H, B, K sont situés sur un même cercle.
(AB) est la médiatrice de [HK] donc par symétrie :

angle AHK=AKB=90°

Les 2 tr AKB et AHB sont rect. en K et H donc inscrits ds le cercle ayant pour diam. leur hypo [AB].
En déduire que : l'angle HKA = l'angle HBA-->ils sont inscrits ds le cercle de daim [AB] et interceptent le même arc.



c)Démontrer de même que : l'angle ALH = l'angle ACH :

ils ont complémentaires de 2 angles égaux : HKA et HBA.


d)Démontrer que les triangles CAB et LHK sont de même forme.

Ils ont 3 angles égaux (alors que 2 suffisent)


Etablir que le rapport de similitude du triangle ABC au triangle LHK est "k = (2AH)/BC".


Le rapport des côtés est :

k=LH/CA=LK/CB=..(1)



Mais ds le tr LHK rect en K , le mileu A de l'hypo est équidistant des 3 sommets donc AL=AH=AK donc LK=2AH

(1) donne : k=LK/CB=2AH/CB

J'envoie.

[bernie]

1°)On se propose de démontrer que :
PM x PN = PA x PB (1)


a)Pour cela, écrire l'égalité à démontrer sous la forme PM/PA = ... ou PM/PB = ...

(1) correspond à :

PM/PA=PB/PN (2)

ou PM/PB=PA/PN

b)Déterminer alors des triangles de même forme dont les côtés interviennent dans les rapports du a)

Pour arriver à (2) on va montrer que les tr PMB et PAN sont semblables.

angle ANM=ABM (incrits ds un cercle et interceptant...)

angle P commun.

Donc semblables donc égalité de rapports : PM/PA=PB/PN soit PM*PN=PA*PB



2°)Exprimer le produit PM x PN en fonction de R et de la distance PO.

Tu traces une 3ème droite (PO) qui coupe le cercle en C et D (C est entre A et M sur ta figure).

On peut montrer comme on vient de le faire que :

PM*PN=PA*PB=PC*PD

Mais PC=PO-CO=PO-R et PD=PO+OD=PO+R

Donc PC.PD=(PO-R)(PO+R)=PO²-R²

Donc PM*PN=PA*PB=PO²-R²

Bon DS.

A+

[Anonyme]

Merci beaucoup Bernie apparement j'ai raissoné pariel que toi pour le premier
Ca va beaucoup m'aider
A la prochaine merci encore

[Anonyme]

bonjour tout le monde!!
vous pouriez maider svp!!

ABC est un triangle quelconque
~ Le point O est le centre du cercle circonscrità ABC
~ H est son orthocentre et G son centre de gravité
~ M es le milieu du segment [BC]
~ [AD] est un diamètre du cercle

1) Démontrer que le segment [HO] est une médiane du triangle AHD
2) Démontrer que les points H, G, O sont alignés.


PS : la question 1 j'ai reussi a la faire facilement!! mais c'es la question qui pose probleme!! coment prouver que ces points sont alignés!!!!!merci bcp d'avance!!

Joana

[Sasuke_Uchina]

il y a une démonstration avec les nombres complexes.

soit O ( centre du cercle circonscrit) l'origine . Ainsi les nombres a,b,c ont le meme module.

on a et on pose 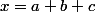, et on se tache de démontrer que x est l'orthocentre du triangle. pour cela on montre que et
sont imaginaires purs ( sachant que a , b, c de meme module )

ainsi on a h=3g , soit OH=3OG

Mais j'aimerais voir une démonstation avec une méthode différente