Pouvez vous m'aider pour cet exercice:
soit la sphere S de centre A(2,-1,3) et de rayon 3.
M(x,y,z) est un point de l'espace.
1. expriimer AM^2 en fonction de x, y et z.
2. determiner une equation de S.
3.de cette equation, deduire les coordonnees des point J et K intersections de S et de l'axe des cotes.
MERCI D'AVANCE!!
Geometrie
7 messages
- Page 1 sur 1
Je ne sais pas du tout quoi faire, j'ai juste penser à faire cela:
1.on a A(2,-1,3) et M(x,y,z)
vecteur AM (x+2,y+1,z-3)
AM^2=(x+2)^2+(y+1)^2
APRES JE NE SAIS PAS COMME FAIRE, PEUT ON UTILISER L'IDENTITE REMARQUABLE?
2. Equation de la sphère: (x+2)^2+(y+1)^2+(z-3)^2=9.
3.POUR CETTE QUESTION JE SAIS PAS QUOI FAIRE
merci!!
1.on a A(2,-1,3) et M(x,y,z)
vecteur AM (x+2,y+1,z-3)
AM^2=(x+2)^2+(y+1)^2
APRES JE NE SAIS PAS COMME FAIRE, PEUT ON UTILISER L'IDENTITE REMARQUABLE?
2. Equation de la sphère: (x+2)^2+(y+1)^2+(z-3)^2=9.
3.POUR CETTE QUESTION JE SAIS PAS QUOI FAIRE
merci!!
salut,
il y a des erreurs
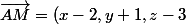)
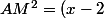^2+(y+1)^2+(z-3)^2)
si M(x;y;z) appartient à (S)AM=r
donc AM²=r²
equation de S:^2+(y+1)^2+(z-3)^2=3^2) donc
donc
equation de S :^2+(y+1)^2+(z-3)^2=9)
l'axe des côtes a pour equation x=0 et y=0 donc il suffit de remplacer x et y par 0 dans l'equation de la sphere
4+1(z-3)²=9
(z-3)²=4
(z-3)²-(2)²=0
(z-3-2)(z-3+2)=0
(z-5)(z-1)=0
z=5 ou z=1
donc les coordonnées sont J(0,0,1) et K(0,0,5)
A+
Je ne sais pas du tout quoi faire, j'ai juste penser à faire cela:
1.on a A(2,-1,3) et M(x,y,z)
vecteur AM (x+2,y+1,z-3)
AM^2=(x+2)^2+(y+1)^2
APRES JE NE SAIS PAS COMME FAIRE, PEUT ON UTILISER L'IDENTITE REMARQUABLE?
2. Equation de la sphère: (x+2)^2+(y+1)^2+(z-3)^2=9.
3.POUR CETTE QUESTION JE SAIS PAS QUOI FAIRE
il y a des erreurs
2. determiner une equation de S.
si M(x;y;z) appartient à (S)AM=r
donc AM²=r²
equation de S:
equation de S :
3.de cette equation, deduire les coordonnees des point J et K intersections de S et de l'axe des cotes.
l'axe des côtes a pour equation x=0 et y=0 donc il suffit de remplacer x et y par 0 dans l'equation de la sphere
4+1(z-3)²=9
(z-3)²=4
(z-3)²-(2)²=0
(z-3-2)(z-3+2)=0
(z-5)(z-1)=0
z=5 ou z=1
donc les coordonnées sont J(0,0,1) et K(0,0,5)
A+
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
