Géométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Rayanne
- Messages: 4
- Enregistré le: 12 Fév 2018, 20:25
-
 par Rayanne » 12 Fév 2018, 21:04
par Rayanne » 12 Fév 2018, 21:04
Bonsoir,
On a trois points

et la fonction (scalaire)
http://dictionnaire.sensagent.leparisie ... niz/fr-fr/=\sum_{i = 1}^{n}\alpha_i\vec(MA_i))
-Je dois trouver

et

tel que

et

j'ai facilement trouvé avec chasles

et

après on me demande de calculer
 = \alpha\left \| MA \right \|^{2}+\beta\left \| MB \right \|^{2})
pour en déduire ensuite
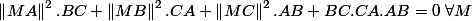
et c'est là que je bloque. J'ai essayé avec la formule du barycentre G avec
 = \varphi(G) + \left \| MG \right \|^{2})
mais je n'arrive nul part.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Fév 2018, 22:22
par Pseuda » 12 Fév 2018, 22:22
Bonsoir,
A mon avis, c'est :

et

.
Sinon, dans ton égalité
 = \alpha\left \| MA \right \|^{2}+\beta\left \| MB \right \|^{2})
, on peut décomposer
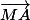
en

et
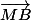
en

.
-
Rayanne
- Messages: 4
- Enregistré le: 12 Fév 2018, 20:25
-
 par Rayanne » 12 Fév 2018, 22:43
par Rayanne » 12 Fév 2018, 22:43
Pseuda a écrit:Sinon, dans ton égalité, on peut décomposer
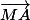
en

et
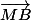
en

.
Merci pour votre aide. Je trouve bien le résultat voulu en décomposant MA & MB. Bonne soirée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 122 invités
en
et
en
.