Voilà j'ai un dm à faire pour jeudi et j'avoue avoir un peu de mal.
Soit ABCD un tétraèdre. On appelle I le milieu de [AB], J le milieu de [AC], K le centre de gravité de BCD et L le symétrique de
D par rapport à A.
Le but de cet exercice est de savoir construire la section du tétraèdre avec le plan (KIJ) et d'expliquer comment réaliser cette construction sur un solide non déformable en fournissant un programme de construction accompagné des justifications utiles.

1) Enoncer les affirmations 1 et 2 et les théorèmes 1 et 2 de façon à ce que les deux déductions soient exactes.
Affirmation 1
Ici je comptais tout d'abord partir sur la relation de Chasles dans un parallélogramme mais je me suis dis que je pouvais également le faire comme cela :
Affirmation :
Donc le théorème que j'ai utlisé c'est Chasles
Affirmation 2
Là j'ai mis : B, C, D sont trois points du plan. Dire que K est le centre de gravité du triangle BCD revient à dire que
D'après la fonction vectorielle de Leibniz pour tout point L on a
4)Sur le dessin 1, représenter en rouge la section du tétraèdre avec le plan (KIJ).
Je pense avoir reussis
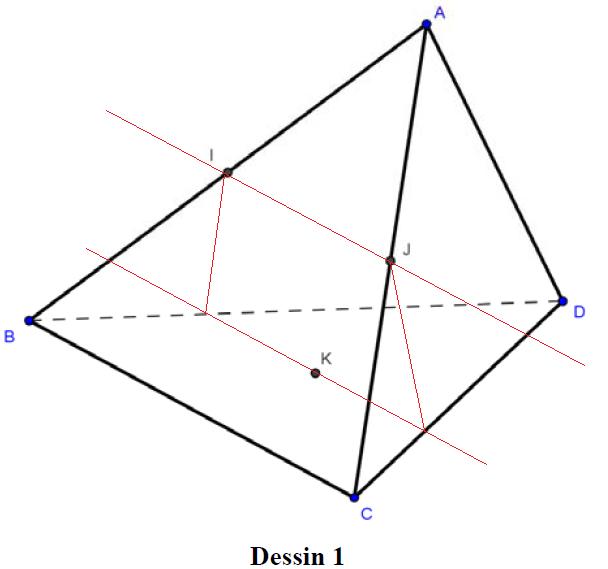
3)Expliquer, à l'aide d'un programme de construction accompagné des justifications utiles, comment réaliser cette construction sur un solide non déformable.
N.B. : Le point L présent dans l'étude « théorique » n'est pas accessible dans cette nouvelle situation, mais l'étude reste valable.
Là je bloque. J'ai lu sur le forum des exercices à peu près similaires mais je ne comprends pas trop ce que je dois réellement faire. J'ai tracé (IJ) et je sais que cette droite est la droite des milieux donc (IJ) (BC) ; j'ai ensuite pensé tracer la parallèle à (BC) passant par K mais je ne sais pas vraiment où cela me mène.
Voici le pdf pour peut être plus de clarté fichier pdf
Merci d'avance pour vos réponses qui je l'espère sauront m'aider :happy2:
