Besoin d'aide sur exercice de Géométrie dans l'espace : les réponses en italiques sont les miennes, je ne suis pas certaines et le reste je ne sais pas le faire
Désolé d'avance, ne sachant pas faire les flèches au dessus des vecteurs, j'écris "Vecteur" devant chaque.
ABCD est un tétraèdre.
On définit les points E, F et G par les égalités :
Vecteur AE + Vecteur DE = 0 ;
Vecteur AF - Vecteur BF - Vecteur CF = Vecteur nul 0 ;
Vecteur BG + Vecteur CG + Vecteur DG = Vecteur nul 0
1. a. Que peut on dire du point E ? E est le milieu de (AD)
b. A quels plans appartiennent les points F et G ? Justifier.
2. a. Exprimer Vecteur AE en fonction de Vecteur AD. Vecteur AE = Vecteur AD + Vecteur DE
b. Exprimer Vecteur AF dans la base (Vecteur AB, Vecteur AC).
c. En déduire l'expression du Vecteur EF dans la base (Vecteur AB, Vecteur AC, Vecteur AD).
3. a. Exprimer Vecteur AG dans la base (Vecteur AB, Vecteur AC, Vecteur AD).
b. En déduire que les points E, F et G sont alignés.
Merci d'avance pour vos réponse !
DM - Géométrie dans l'espace n °1 ; Pour vendredi
4 messages
- Page 1 sur 1
Re: DM - Géométrie dans l'espace n °1 ; Pour vendredi
Bonjour,
"Plans" est au pluriel, donc il faut trouver un plan pour F et un plan pour G. C'est assez "évident" si vous avez fait un schéma (à condition de connaitre la définition du "centre de gravité d'un triangle").
Vous avez la somme de trois vecteurs qui donne un vecteur nul. Que peut-on en déduire pour ces trois vecteurs ? Comme ces vecteurs ont tous un point en commun, cela donne alors le résultat.
Pour a, vous ne répondez pas à la question : "en fonction du vecteur AD" donc uniquement de celui-là (vous ne pouvez pas utiliser le vecteur DE). Mais puisque E est le milieu... ?
Pour b : Avec un schéma, on "voit" tout de suite le résultat (qu'est-ce que la forme ABFG...), mais "voir" n'est pas une démonstration.
Puisque vous avez AF en fonction de BF et de CF (en vecteurs), utilisez Chasles pour faire apparaître AB et AC et faire disparaître BF et CF...
Pour c. c'est assez direct en écrivant le vecteur EF avec une relation de Chasles
Pour a., même technique que la question précédente : faites apparaître le vecteur AG dans la relation donnée par l'énoncé en utilisant Chasles.
Pour b. Je n'ai pas fait l'exercice (juste donné les indications), donc je ne sais que dire ici, mais il y a fort à parier qu'on puisse s'en tirer avec une colinéarité de vecteurs : vous avez déjà identifié EF, faites de même avec le vecteur EG.
clemfnc a écrit:1. a.
b. A quels plans appartiennent les points F et G ? Justifier.
"Plans" est au pluriel, donc il faut trouver un plan pour F et un plan pour G. C'est assez "évident" si vous avez fait un schéma (à condition de connaitre la définition du "centre de gravité d'un triangle").
Vous avez la somme de trois vecteurs qui donne un vecteur nul. Que peut-on en déduire pour ces trois vecteurs ? Comme ces vecteurs ont tous un point en commun, cela donne alors le résultat.
clemfnc a écrit:2. a. Exprimer Vecteur AE en fonction de Vecteur AD. Vecteur AE = Vecteur AD + Vecteur DE
b. Exprimer Vecteur AF dans la base (Vecteur AB, Vecteur AC).
c. En déduire l'expression du Vecteur EF dans la base (Vecteur AB, Vecteur AC, Vecteur AD).
Pour a, vous ne répondez pas à la question : "en fonction du vecteur AD" donc uniquement de celui-là (vous ne pouvez pas utiliser le vecteur DE). Mais puisque E est le milieu... ?
Pour b : Avec un schéma, on "voit" tout de suite le résultat (qu'est-ce que la forme ABFG...), mais "voir" n'est pas une démonstration.
Puisque vous avez AF en fonction de BF et de CF (en vecteurs), utilisez Chasles pour faire apparaître AB et AC et faire disparaître BF et CF...
Pour c. c'est assez direct en écrivant le vecteur EF avec une relation de Chasles
clemfnc a écrit:3. a. Exprimer Vecteur AG dans la base (Vecteur AB, Vecteur AC, Vecteur AD).
b. En déduire que les points E, F et G sont alignés.
Pour a., même technique que la question précédente : faites apparaître le vecteur AG dans la relation donnée par l'énoncé en utilisant Chasles.
Pour b. Je n'ai pas fait l'exercice (juste donné les indications), donc je ne sais que dire ici, mais il y a fort à parier qu'on puisse s'en tirer avec une colinéarité de vecteurs : vous avez déjà identifié EF, faites de même avec le vecteur EG.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM - Géométrie dans l'espace n °1 ; Pour vendredi
Merci pour votre réponse,
Je vais essayer de ma débrouiller avec ça, on verra si j'y arrive.
Cependant, qu'est ce que le centre de gravité ? car pour moi G était le centre de gravité du triangle BCD en m'appuyant sur mon annabac de maths mais je ne sais pas comment répondre à la question b du coup sans comprendre cela.
Je vais essayer de ma débrouiller avec ça, on verra si j'y arrive.
Cependant, qu'est ce que le centre de gravité ? car pour moi G était le centre de gravité du triangle BCD en m'appuyant sur mon annabac de maths mais je ne sais pas comment répondre à la question b du coup sans comprendre cela.
Re: DM - Géométrie dans l'espace n °1 ; Pour vendredi
Si vous ne savez pas ce qu'est le centre de gravité, ce n'est pas grave vous pouvez faire tout l'exercice sans cela (en faisant comme je l'ai indiqué).
C'et juste que si vous saviez ce que c'était vous auriez tout de suite l'idée du plan auquel appartient G.
Le centre de gravité du triangle est l'intersection des médianes, et il se trouve qu'alors on a exactement ceci : si G est ce centre pour ABC,
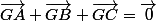
C'et juste que si vous saviez ce que c'était vous auriez tout de suite l'idée du plan auquel appartient G.
Le centre de gravité du triangle est l'intersection des médianes, et il se trouve qu'alors on a exactement ceci : si G est ce centre pour ABC,
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
