DM - Géométrie dans l'espace n °2 ; Pour vendredi

[clemfnc]

Besoin d'aide sur un exercice de géométrie dans l'espace :

Soit d et d' les droites de représentations paramétriques :

x = 7 + 4t
y = 20 + t
z = 2 + 2t
avec t appartenant à R

et

x = 5 + 2k
y = 2 - 3k
z = 1 + k
avec k appartenant à R

Démontrer que les droites d et d' sont sécantes en un point A dont on déterminera les coordonnées.

J'ai déjà trouver des réponses en faisant :
7+4t = 5+2k
20+t = 2-3k
2+2t = 1+k
Cependant, quand je mets les valeurs de t et de k trouvées au sein de mes représentations paramétriques, je ne trouve pas les mêmes coordonnées pour le point A

Merci d'avance pour vos réponses !

[hdci]

Bonjour,

Commençons par là : qu'avez-vous trouvé pour t et k ?

[clemfnc]

Bonjour,

J'avais :
t = -1/3
k = 1/3

[hdci]

Donc c'est normal que vous ne trouviez pas le même point A, car ce n'est pas la solution du système.

Quand vous avez trouvé les valeurs de t et de k, pensez à les remplacer dans votre système pour "vérifier" ! C'est un réflexe que vous devez avoir quand vous avez le temps.
Ici, on a avec -1/3 et 1/3, rien qu'avec la ligne 20+t=2-3k, c'est-à-dire t=-18-3k : k multiplié par 3 sera entier, on prend l'opposé et on soustrait 18, le résultat est donc entier, or t=-1/3... C'est donc faux.

Revoyez la résolution de votre système !

[clemfnc]

Merci beaucoup,

Je vais alors essayer à nouveau de résoudre mon système, mais je pense que je m'y prend mal.

[hdci]

Une technique pour résoudre le système : "par substitution".

Vous prenez une ligne où il est facile d'exprimée une inconnue en fonction de l'autre (ici par exemple, avec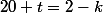 il est facile d'en déduire une formule simple en fonction de k).

Vous utilisez alors cette formule pour remplacer t dans l'une des deux autres équations : cela vous permet de trouver k.

Vous revenez alors à et vous remplacez k par ce que vous avez trouvé : cela donne t.

Vous utilisez enfin la dernière équation en remplaçant t et k : si vous obtenez bien une égalité, c'est OK, sinon c'est soit que vous avez fait une erreur, soit que les deux droites ne sont pas sécantes.

[clemfnc]

Merci beaucoup, j'ai envi trouvé mon erreur, j'ai juste inversé deux chiffre lors d'une division et cela à faussé mon résultat.

Au final, on a t = -3 et k = -5

[vam]

bonjour
pas sympa pour les aidants qui passent du temps...poster le même sujet ici alors que tu avais de l'aide ailleurs...