Forme trigonomètrique d'un complexe

[clac-mer2]

Bonsoir, dans mon TP on me demande, de donner ce(s) nombre(s) complexe(s) sous forme algébrique puis trigonométrique.

formule de base :


On associe alors à cette grandeur "a" le nombre complexe, noté A, de module A et d'argument thêta.



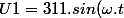Merci d'avance d'avoir pris le temps de me lire.

[XENSECP]

Oui euh quelle est la question ?

[Florélianne]

Bonjour,
Ce n'est pas la question que je demande, je l'ai trouvée et comprise, mais le sens de tout ça...
je comprend mal la liaison entre a(t) et A qui serait un point donc on aurait pu croire que son affixe était a(t) mais ça ne colle pas avec la suite...
A a-t-il pour affixe z=x+iy ?
mais que représente le A dans a(t) = A sin(oméga*t + thêta) ?
Difficile de donner la forme algébrique ou trigonométrique d'un nombre complexe qu'on ne comprend pas !
Très cordialement

[clac-mer2]

Bonsoir désolé de ne répondre que maintenant, A est la valeur maximale ou efficace en électronique, et en réalité la formule possède un thêta qui est enfaite l'argument du complexe et A est son module.
J'avais simplement mal lu l'énoncé :girl2:
Merci quand même