Forme canonique et tableau de variation

[alexialj]

Bonjour tout le monde je suis en premiere ES et je galère sur un exercice de maths qui est à rendre pour demain... j’aimerais beaucoup que vous m’aidiez voici l’énoncé :

Établir le tableau de variation des fonctions f et g sur l’intervalle [-10;10] sachant que :

f(x)=5 [(x-5)*2 +3] et g(x) = -1/2 (x+ 4)*2 -2

Merci d’avance

[capitaine nuggets]

Salut !

Quel sont les variations de la fonction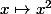 sur ?
Quel sont les variations de la fonction sur ?
Quel sont les variations de la fonction +3 sur ?
Déduis-en alors les variations de la fonction sur .

[alexialj]

Je suis très nulle en maths et j’ai donc pas compris ce que vous m’avez dit

[capitaine nuggets]

C'est pas une question d'être bon ou nul en maths : il s'agit de savoir si tu connais ton cours ou non...
Etant donné que c'est à rendre pour demain, j'espère que tu ne vas pas attendre passivement une réponse parce que ça n'arrivera pas : le but de ce forum n'est pas de faire tes devoirs à ta place.

Tu devrais pouvoir répondre à ma première question : c'est du niveau 2nde, on voit ça dans les fonctions de références. Si ce n'est pas le cas, je t'encourage à revoir ou même à garder ouvert ton cours parce que si tu n'es pas capable de répondre à une simple question comme la première que j'ai posé, tu risques d'avoir des difficultés pour faire tes exos.

[alexialj]

Sans être vulgaire sa m’enquiquine les maths alors je sais mon cours mais pour l’appliquer je ne comprend pas

[pascal16]

sa m’enquiquine les maths alors je sais mon cours mais pour l’appliquer je ne comprend pas

Faudrait l'encadrer cette réponse

[alexialj]

Quelle réponse ?

[capitaine nuggets]

Oui, je conçois parfaitement que certaines personne s'en moque des maths, cependant il y a quand même le BAC à la fin de la terminale donc tu dois quand même savoir un minimum de chose (dis-toi que c'est de la culture générale). Si tu sais ton cours, il est possible de t'aider à l'appliquer : c'est justement ce que j'ai essayé de faire en détaillant les étapes pour établir les variations de f.

Du coup, quelles sont les variations de la fonction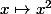 sur ? Si tu préfères, quelles sont les variations de la fonction sur l'intervalle ?

[pascal16]

forme canonique
g(x) = -1/2 (x+ 4)² -2
donc
g(x) = -1/2 x² + ....
de la forme ax²+bx+c avec a<0

la courbe est donc en forme d'un U à l'envers
elle passe donc par un maximum

g(x) = -1/2 (x+ 4)² -2
x+ 4=0 pour x=-4
elle atteint ce maximum pour x=-4
ce maximum vaut f(-4) = -2

PS pour Captain : en début de 1ES, je pense que personne n'a vu de composée de fonctions, il me semble qu'aucune formalisation des composées n'est au programme. La réciproque est juste évoquée pour passer de exp à ln.

[alexialj]

Merci beaucoup pascal mais la forme canonique comment trouve on a b et c puisque c’est pas la même forme

[alexialj]

Je comprend pas capitaine nuggets

[pascal16]

cas général :

équation développée :
f(x) = ax²+bx +c
forme canonique :


le "a" est le même dans les deux écritures, on a pas besoin de le calculer !

a>0 : la courbe est en forme de U
a<0 : la courbe est en forme de U à l'envers

[alexialj]

j’ai compris merci beaucoup

[alexialj]

Juste pour f(x) x= 5 en minimum c’est sa ?

[alexialj]

Oula je bloque

[alexialj]

Uppppp

[capitaine nuggets]

Etant donné que c'est à rendre pour demain, j'espère que tu ne vas pas attendre passivement une réponse parce que ça n'arrivera pas : le but de ce forum n'est pas de faire tes devoirs à ta place.

Pas de "up", je croyais qu'on s'était compris : tu n'es pas la seule à avoir besoin d'aide (sans parler du fait que d'autres s'y sont pris plus tôt que toi...) et les gens ont une vie en dehors du forum : tout le monde n'est pas dispo 24/24h, 7/7j et encore moins pour faire tes devoir à ta place. Donc inutile de monopoliser de la place sur le forum, ça ne marchera pas. Je trouve que pascal16 a été assez généreux avec toi, remercie en relisant et utilisant ce qu'il t'a dit, merci.

On peut voir ici... d'ailleurs que ton but n'est clairement pas de chercher ton exercice mais bien de trouver quelqu'un d'assez bête pour faire tes devoirs à ta place.