Fonctions et suites - terminale

[romani01]

c'était au cas où on l'utilisait.
bon je vais revoir mon hérédité, en tous cas merci beaucoup de ton aide Romani c'était très gentil de ta part, bonne continuation

J'attends pour voir ce que tu as fait.

[Anonyme]

mais pour l'hérédité normalement je dois faire 0(strict inférieur à) y(n+1)(inférieur ou égal a) 1 non ?

[Anonyme]

Salut Ababo.
Tout d'abord on te dit que tend vers 0 quand h--->0 donc :
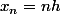
mais on sait que f'(x)=-2xf(x) donc .Tu remplaces dans et tu obtiens et tu connais .Tu remplaces et tu mets en facteur.

et ceci c'est pour quelle question ?
et ma question 3 et la 4 sont-elles correctes ?

[romani01]

mais pour l'hérédité normalement je dois faire 0(strict inférieur à) y(n+1)(inférieur ou égal a) 1 non ?

C'est ce que tu démontrer.
En partant de on multiplie les 2membres par 0,02 on obtient
on multiplie par -1 et -1<=-0,02n<0 on ajoute 1 et
et on a hypothèse de récurrence 0<yn<=1;on multiplie les deux inégalités membre à membre ...............

[Anonyme]

C'est ce que tu démontrer.
En partant de on multiplie les 2membres par 0,02 on obtient
on multiplie par -1 et -1<=-0,02n<0 on ajoute 1 et
et on a hypothèse de récurrence 0<yn<=1;on multiplie les deux inégalités membre à membre ...............

quelles sont les deux inégalités ?
je ne comprends pas...

[Anonyme]

tu es surement parti romani alors je me debrouillerai, merci beaucoup pour tout et aurevoir :)

[romani01]

et ceci c'est pour quelle question ?
et ma question 3 et la 4 sont-elles correctes ?

Ca ,c'etait pour écrire donc
.
Justement tes questions 3 et 4 n'étaient pas bonnes ,tu n'avais pas pensé à remplacer f'(xn) en utilisant f'(x)=-2xf(x) c'est à dire f'(xn)=-2xnf(xn).

[romani01]

quelles sont les deux inégalités ?
je ne comprends pas...

Inégalité 1 :0<1-0,02n<=1(qu'on vient de démontrer)
Inégalité 2:0<yn<=1 (hypothèse de récurrence)
on multiplie (1) par (2) et 0<yn(1-0,02n)<=1 et comme y(n+1)=yn(1-0,02n) on a
.Ce qu'il fallait démontrer.

[Anonyme]

ah d'accord je comprends mieux maintenant, et pour les questions 3 et 4 aussi

eh bien je l'ai déjà dis mais je le redis, encore merci romani de m'avoir accordé de ton temps
Je te souhaite une bonne continuation
et aussi une bonne année, aurevoir :)

[romani01]

ah d'accord je comprends mieux maintenant, et pour les questions 3 et 4 aussi

eh bien je l'ai déjà dis mais je le redis, encore merci romani de m'avoir accordé de ton temps
Je te souhaite une bonne continuation
et aussi une bonne année, aurevoir

Pardon,dans tout ça j'ai oublié de te souhaiter BONNE ANNEE ET SURTOUT BONNE SANTE.