Bonjour a tous voici mon dm de maths pouvez-vous m'aidez à le faire car malgès mes absences en cours je n'y suis pas parvenue à le faire.
Pour chaque fonction f, on étudiera ses variations, on déterminera ses limites (à reporter dans le
tableau de variations) et on indiquera les éventuelles asymptotes à la courbe.
1. La fonction f est définie sur ℝ\{1} par f(x) = x^2+2x-1/x-1
2. La fonction f est définie sur ℝ par f(x) = (x – 2)e^x
(Pour déterminer la limite de f en -∞, on utilisera l’indication : lim xe^x=0).
-∞
Merci.
La fonction
8 messages
- Page 1 sur 1
Re: La fonction
mathelot a écrit:bonjour,
pour la question 1. il s'agit de?
bonjour, oui voila c'est sa.
Re: La fonction
Carpate a écrit:malgré mes absences en cours
Étonnant !
Car problème familiale tout simplement !
Re: La fonction
Tu a certainement voulu écrire le contraire :
car (malgré) à cause de mes absences en cours je n'y suis pas parvenue à le faire.
Donc domaine de définition de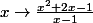
calcul de sa dérivée
limites de en
en 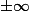 et au voisinage de x = 1
et au voisinage de x = 1
tableau de variation
car (malgré) à cause de mes absences en cours je n'y suis pas parvenue à le faire.
Donc domaine de définition de
calcul de sa dérivée
limites de
tableau de variation
Re: La fonction
Carpate a écrit:Tu a certainement voulu écrire le contraire :
car (malgré) à cause de mes absences en cours je n'y suis pas parvenue à le faire.
Donc domaine de définition de
calcul de sa dérivée
limites deen
et au voisinage de x = 1
tableau de variation
Oui voila c'est sa j'aurai du écrire comme ça désolé.
En tout merci pour votre aide.
Re: La fonction
Y'a pas de quoi être désolé !
Dis nous plutôt où tu en es :
domaine de définition
valeur trouvée pour la dérivée
etc
Dis nous plutôt où tu en es :
domaine de définition
valeur trouvée pour la dérivée
etc
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
