Fonction

par **DODO59** » 14 Oct 2006, 08:20

Bonjour,

Je suis en 1ère S et j'ai besoin d'aide en math.
Est-ce que quelqu'un peut m'expliquer l'exercice suivant SVP :

a) Vérifier que pour tout réel x, on a x² + 3x + 3 = (x + 1)² + x + 2

et en déduire que pour tout x de I,

{x²+3x+3}/{(x +1)² } > 1

b) Démontrer que pour tout x de I, f(x)
c) Interpréter graphiquement des deux ingalités obtenues et hachurer sur un graphique la région du plan dans laquellle doit se situer la courbe f.

Données: f(x) = {(x-1) (x²+3x+3)}/(x+1)² ou f(x) = ax + b/(x+1) +c /(x+1)²
I = ]-1; plus l'infini [

Merci d'avance

DODO59

par **allomomo** » 14 Oct 2006, 09:17

Salut,

a.

b.

Pour quelles conditions a-t-on :

On sait qu'on doit avoir :
*

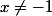
sinon on a 0 en dénominateur.
*

Conclusion :

[center]

[/center]

Remarque :

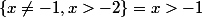
c. Enoncé à vérifier ...

par **DODO59** » 14 Oct 2006, 10:02

merci de m'avoir répondu

pour le petit a) j'ai réussi à le faire par contre pour le b) je passe le x de l'autre côté de l'inéquation* après j'essaie de calculer et je me bloque

* f(x) - x < 0
{ (x-1) (x² + 3x +3)} / { (x+1)² } -x <0

au fait que veut dire le A à l'envers?

merci d'avance

DODO59

par **allomomo** » 14 Oct 2006, 10:04

Salut,

Tu es sûr que c'est

?

par **DODO59** » 14 Oct 2006, 10:14

oui, j'en suis sur c'est dans mon énoncé
x à comme intervalle ]-1 ; plus l'invini[

merci de bien vouloir m'expliquer

par **allomomo** » 14 Oct 2006, 10:19

RE -

Toi tu veux démontrer que

est vraie pour tout x de I.
Or c'est faux, on peut facilement trouver un contre exemple.

Si :

,

et donc on

ce qui est absurde.

-------
Par contre :

est vraie !
-------

Sauf si je me trompe de fonction!

par **DODO59** » 14 Oct 2006, 10:27

je comprend maintenant, mais juste une chose que veux dire le A à l'envers au début, dans ce que vous m'avez marqué?

par **DODO59** » 14 Oct 2006, 10:52

je viens de refaire ce que tu n'avais marqué: c'est à dire si x=0

je trouve f(x) =0

ensuite j'ai recommencé avec si x= -2

ça me donne f(-2)= [(-2-1) * (-2² +3 * -2 +3)} / (-2 +1 )²
je trouve f(-2) = -3 donc -3< -2

ça fait pareil pour x = 4

je voudrais savoir ce que tu en pences

merci d'avance DODO 59

par **allomomo** » 14 Oct 2006, 10:54

bon alors, si c'est vrai => je me trompe de fonction !

par **DODO59** » 14 Oct 2006, 11:00

merci beaucoup pour ton aide et peut -être à une autre fois sur sur le forum

à bientôt

DODO59

Fonction

Fonction

Qui est en ligne