Fonction

[Tiramisu]

Bonjour,
Je suis nouveau sur ce site et j'espère que vous pourrez m'éclairer dans mon problème. Je suis censé trouver la vitesse moyenne maximale d'un motard, celle qu'il ne pourra jamais atteindre même s'il roule très vite.

Je pense avoir une petite idée. La vitesse moyenne maximale, que l'on notera y est la valeur pour laquelle la vitesse moyenne sera toujours inférieure. Par conséquent,

Est-ce juste ?
Merci d'avance pour votre aide.

[Elerinna]

La vitesse moyenne maximale, que l'on notera y est la valeur pour laquelle la vitesse moyenne sera toujours inférieure. Par conséquent,

Est-ce juste ? :hein:

Etudie donc les variations de la fonction sur notamment :

[Tiramisu]

Bonjour Elerinna,

Etudie donc les variations de la fonction sur notamment :

La fonction est croissante sur . Donc comment pourrait on faire pour trouver sa vitesse moyenne maximale ? Quel est le principe ?

Merci pour votre aide.

[Elerinna]

Bonjour Elerinna,


La fonction est croissante sur . Donc comment pourrait on faire pour trouver sa vitesse moyenne limite ? Quel est le principe ?

Merci pour votre aide.

Sa vitesse moyenne limite n'est que la borne maximale de en . Trouve cette limite (Cf. un cours).

[Tiramisu]

J'ai tracé la représentation graphique de la fonction f. Cela donne une fonction constante avec y=180. Cette limite est un peu comme le mur infranchissable n'est-ce pas ? Mais comment fais-t-on pour trouver par le calcul que cette limite est 180?

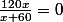
J'ai essayé avec Sauf que ce n'est pas la bonne solution. :triste:

[Tiramisu]

Si j'ai bien compris :
. Sauf que c'est une forme indéterminée. Comment calcules-t-on ce genre de résultats svp ?

EDIT : C'est bon, je pense avoir trouver grâce a d'autres discussions sur le forum. Merci beaucoup Elerinna pour votre grande aide :happy3:

[Tiramisu]

Est-ce que je peux dire que le résultat est ?