Fonction et polynôme de degré 4
7 messages
- Page 1 sur 1
Fonction et polynôme de degré 4
Bonjour j'ai un exercice à faire sur les fonctions et polynome de degré 4 voici l'énoncé : soit f la fonction définie par f(x) = 1/x (fonction inverse) et h sa courbe représentative dans un repère orthonomal. M est un point de h d'abscisse x et I est un point quelconque de coordonnées (alpha;beta). Démontrer que: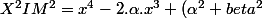x^2-2.beta.x + 1) (ca j'ai réussi). Ensuite l'énoncé dit : on note p le polynôme de degré 4 défini par p(0)= 1 et
(ca j'ai réussi). Ensuite l'énoncé dit : on note p le polynôme de degré 4 défini par p(0)= 1 et  = x^2IM^2 si x # 0) . Démontrer qu'il existe deux points, et deux seulement, pour lesquels
. Démontrer qu'il existe deux points, et deux seulement, pour lesquels =(x^2 - \alpha.x +h)^2) (h un réel quelconque). On notera F et F' ces deux points (F d'abscisse positive). C'est ici que je n'y arrive pas. Merci d'avance à ceux qui pourront m'aider.
(h un réel quelconque). On notera F et F' ces deux points (F d'abscisse positive). C'est ici que je n'y arrive pas. Merci d'avance à ceux qui pourront m'aider.
Oplya a écrit:Bonjour j'ai un exercice à faire sur les fonctions et polynome de degré 4 voici l'énoncé : soit f la fonction définie par f(x) = 1/x (fonction inverse) et h sa courbe représentative dans un repère orthonomal. M est un point de h d'abscisse x et I est un point quelconque de coordonnées (alpha;beta). Démontrer que:(ca j'ai réussi). Ensuite l'énoncé dit : on note p le polynôme de degré 4 défini par p(0)= 1 et
. Démontrer qu'il existe deux points, et deux seulement, pour lesquels
(h un réel quelconque). On notera F et F' ces deux points (F d'abscisse positive). C'est ici que je n'y arrive pas. Merci d'avance à ceux qui pourront m'aider.
Développe
Si je ne me suis pas trompé , on arrive à deux points F'(-1;0) et F(1;0)
Oplya a écrit:Je trouveje ne vois pas ce que tu veux dire par identifier :
C'est pourtant une opération classique :
2 polynômes sont identiques si quelques soient les valeurs de leur variable x, ils ont la même valeur. Cela implique qu'ils soient de même degré et que les coefficients des termes de même degré soient égaux.
Je trouve :
Pour identifier
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
