Fonction inversible

[rorororo1991]

Bonjour,

Par définition, une fonction est inversible si on peut remplacer x par y et inversément et obtenir ainsi une nouvelle fonction.

Pour cette fonction:
f(x) = x² + 3x + 2

Je remplace x par y donc j'obtiens y² + 3y + 2 = x
Mais ceci n'est plus une fonction car on ne sait pas isoler y ? Donc la fonction n'est pas inversible?

Merci.

[Luc]

Bonjour rorororo1991,

sais-tu résoudre une équation du deuxième degré?
En l'occurence, pour x fixé,
d'inconnue y.

En fait, la notion d'inversibilité que tu évoques pour les fonctions s'appelle la bijectivité. Et pour garantir cette bijectivité, il faut que chaque x ait une image distincte par f (sinon, on ne peut pas définir l'inverse de f car une telle "fonction" aurait deux images pour f(x)). Généralement, on est donc amené à considérer f non pas sur R tout entier mais seulement sur des intervalles où elle est bijective.

En l'occurrence, des intervalles vont apparaître naturellement en fonction du signe du discriminant de l'équation d'inconnue y.

Bon courage,
Luc

[rorororo1991]

Merci
Mais puisqu'ici on a une fonction du second degré,
pour un même f(y) on aura deux valeurs de y différentes (deux racines annulant la fonction) donc la fonction est bien surjective?

Donc on peut considérer qu'une fonction est inversible si elle est bijective? donc qu'elle ne l'est pas si elle est injective ou surjective?

[Luc]

1.

Merci
Mais puisqu'ici on a une fonction du second degré,
pour un même f(y) on aura deux valeurs de y différentes

Pas forcément, cela dépend du signe du discriminant que tu dois calculer (soit 2 racines simples, soit une racine double, soit pas de racine réelle). On voit donc apparaître une condition sur x.
2.

Donc on peut considérer qu'une fonction est inversible si elle est bijective? donc qu'elle ne l'est pas si elle est injective ou surjective?

Bijective est équivalent à (injective et surjective). Mais il faut toujours spécifier l'ensemble de départ et l'ensemble d'arrivée, sinon cela n'a aucun sens.
3. Je te conseille d'étudier f en faisant un tableau de signes et de tracer son graphe. Ce sera beaucoup plus clair pour comprendre ce dont il est question, et le cas échéant d'envisager l'inverse de f.

Luc

[Luc]

Un bon moyen d'assurer l'injectivité est la monotonie stricte. On a par exemple le résultat suivant :
Si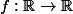 est strictement croissante, alors f est bijective. De plus, la bijection réciproque de f est également strictement croissante. Si tu connais la définition d'un groupe, on dit que l'ensemble des fonctions strictement croissantes de dans muni de la loi de composition des fonctions forme un sous-groupe du groupe des bijections de . L'inverse de f au sens du groupe est sa bijection réciroque.

[chan79]

[quote="Luc"] On a par exemple le résultat suivant :
Si est strictement croissante, alors f est bijective. QUOTE]

Salut
Attention, regarde la fonction arctan

[Luc]

On a par exemple le résultat suivant :
Si est strictement croissante, alors f est bijective. QUOTE]

Salut
Attention, regarde la fonction arctan

arctan est bien bijective vers . Il faut effectivement préciser l'ensemble d'arrivée.
Luc

[chan79]

arctan est bien bijective vers . Il faut effectivement préciser l'ensemble d'arrivée.
Luc

Comme ça, d'accord :lol3: