Fonction homographique

[lololavape]

Bonsoir,
je suis en train de faire un devoir de math avec mon fils qui est en seconde mais j'ai vraiment du mal.

L'ennoncé est le suivant en espérant que l'un d'entre vous pourra m'aider.

Résolution graphique d'une inéquation.
Soit f(x)=(7x+2)/(2-4x)

1) la fonction f(x) est elle homographique? si oui pourquoi ?
2) donnez l'ensemble de définition de f(x) sous forme d'intervalle?
3)étudiez la variation de f(x) sur son ensemble de définition puis donnez son tableau de variation.
4) graphiquement , résolvez a) f(x)<0 b) f(x)>0

j'ai réussi à l'aider sur le reste de son devoir mais pour la partie fonction j'ai vraiment du mal . Help us please

[laetidom]

Bonsoir,

1) sur le net on peut trouver aisément une définition :


si oui, alors pourquoi ? . . .

2) on n'a pas le droit en maths de diviser par 0 donc ici le dénominateur ne doit pas être nul ====> Quelle est donc la valeur interdite à exclure du . . . ?


On peut écrire valeur valeur


3)





: Domaine de Définition de la fonction

[eusebe78]

variation de la fonction: est-elle croissante, décroissante sur quel intervalle. outils à utiliser: dérivée f' (positive= fonction croissant/ négative= fonction décroissante)

Exemple de tableau de variation:



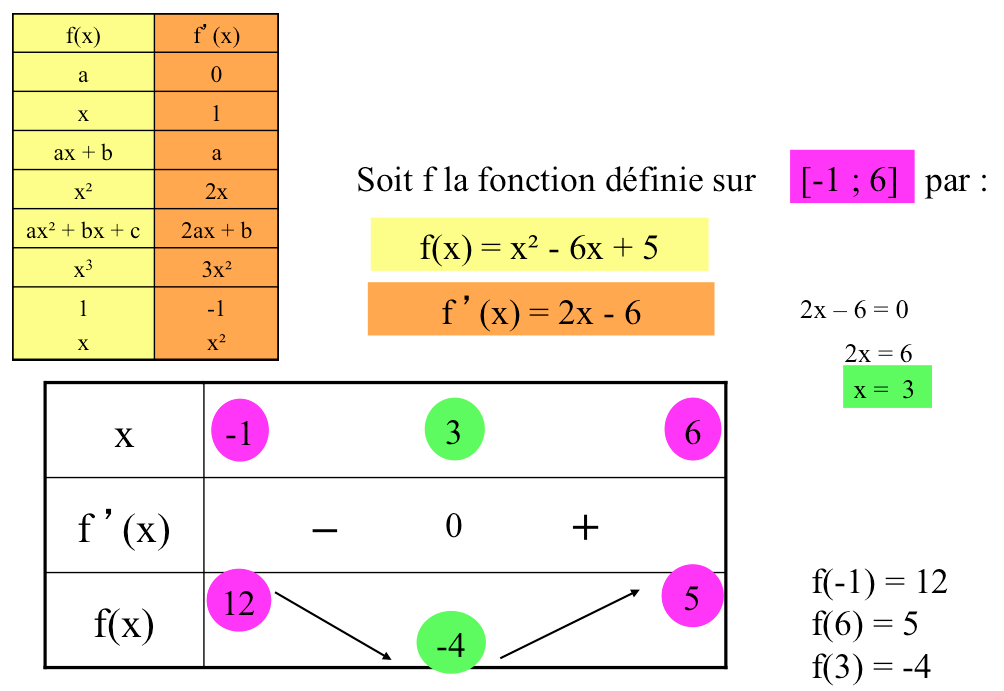
4) Un aperçu des zones où la fonction est positive ou négative

https://www.wolframalpha.com/input/?i=plot(7x%2B2)%2F(2-4x)

[laetidom]

Bonsoir eusebe,

Et oui avec la dérivée c'est très rapide mais le fils de lololavape est en Seconde . . .

[eusebe78]

Oui j'ai compris après coup que la méthode avec les dérivées n'est pas encore utilisée à ce stade.

[laetidom]

:D Oui j'ai compris après coup que la méthode avec les dérivées n'est pas encore utilisée à ce stade.

C'est moins rapide mais ça se fait bien tout de même (la méthode en Seconde) !

Ton information est positive car elle présente l'outil de la classe suivante qui permettra de faire beaucoup de choses intéressantes !

[laetidom]

Comprends-tu lololavape ? :



1) Une fonction affine se présente de la forme suivante : y = ax + b

Est-ce le cas au numérateur et au dénominateur de f(x) . . . ?

numérateur : 7x + 2 ===> Oui car a = 7 et b = 2

dénominateur : - 4x + 2 ===> Oui car a = - 4 et b = 2


Tu peux donc répondre à la première question !

[lololavape]

Oui ça c'est bon

[laetidom]

Oui ça c'est bon

Bonjour,

ok donc pour le 1)

2) Quelle est donc la valeur non autorisée pour f(x) . . . ?

On doit avoir

[lololavape]

donc x different de 1/2
ensemble de def ] -inf;1/2[ U ]1/2;+inf[ est-ce bon ?

[laetidom]

donc x different de 1/2
ensemble de def ] -inf;1/2[ U ]1/2;+inf[ est-ce bon ?

Oui ! On peut l'écrire aussi {} mais ta notation est celle qui convient pour répondre correctement à la question posée !

[lololavape]

par contre je n'arrive pas à etudier la variation et donner son tableau de variation

[laetidom]

par contre je n'arrive pas à etudier la variation et donner son tableau de variation

Une petite aide : http://www.cjoint.com/c/GDblMgQls27

J'ai trouvé la forme canonique : f(x) = et lorsque j'écris que a < b <2 j'obtiens que f(a) < f(b) ce qui signifie que la fonction est croissante :

[lololavape]

je n'arrive pas à résoudre graphiquement la partie 4) de son exercice pour f(x)<0 et f(x)>0 pourriez-vous m'aider

[titine]

je n'arrive pas à résoudre graphiquement la partie 4) de son exercice pour f(x)<0 et f(x)>0 pourriez-vous m'aider

On peut faire tracer la courbe représentative de la fonction f par la calculatrice ou par un logiciel.
Puis on regarde pour quelles valeurs de x on a f(x) négatif (<0)
Autrement dit, quelles sont les abscisses des points de la courbe qui sont situés en dessous de l'axe des abscisses (qui ont une ordonnée négative)
Comprends tu ?

[laetidom]

Bonjour,




quand y = f(x) > 0, la courbe va d'où à où . . . ?

quand y = f(x) < 0, la courbe va d'où à où . . . ?

On peut répondre à ces questions car l'on a déjà réalisé le tableau de variations (question 3) dans lequel on a identifié les limites de la fonction . . .