Bonjour,
Voici un petit problème de 4 questions, que je pense avoir solutionné, sauf pour la dernière question.
Aussi, je vous demande une petite vérification, agrémentée par le tout LaTex :zen:
--- Enoncé ---
On désigne par
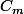
l'ensemble des points
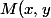)
dont les coordonnées vérifient la relation

:
=0)
,
dans laquelle

est un paramètre. Pour toute valeur de
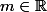
, cette relation définie une fonction

de la variable

.
1°) Etudier, pour toutes les valeurs de

différentes de

et de -1, le sens de variation de de

.
2°) Déterminer l'ensemble des points

pour
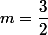
et l'ensemble des points

pour
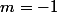
.
3°) Mettre la relation

sous la forme :
+mg(x,y)=0)
, puis résoudre le système de deux équations à deux inconnues

et

:
 & = & 0,\\<br /> g(x,y) & = & 0.<br />\end{array}<br />\right.)
En déduire que,

, la courbe
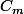
passe par deux points dont les coordonnées sont indépendantes de

.
4°) La courbe
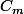
admet deux asymptotes. Calculer, en fonction de

, les coordonnées du point d'intersection

de ces asymptotes. Quel est l'ensemble

des positions de

associé à l'ensemble des valeurs de

?
--- Ma solution ---
La relation

de départ est une relation homographique entre les variables

et

, que l'on transforme en une fonction homographique en isolant

:
=0\Leftrightarrow y=\dfrac{mx+m+3}{x+2m})
1°) Dans le cas général d'une fonction homographique :
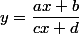
, la fonction dérivée est :
^2})
Dans ce cas particulier, l'expression de la dérivée est :
^2}=\dfrac{(2m-3)(m+1)}{(x+2m)^2})
Comme le dénominateur est un carré, toujours positif, l'étude du sens de variation de

est réduit à l'étude du signe au numérateur de

'.
[CENTER]
(m+1)}&+&0&-&0&+\\<br />\hline{\text{Variations de y}}&\nearrow&0&\searrow&0&\nearrow<br />\end{array})
[/CENTER]
2°) L'ensemble des points pour
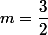
est :
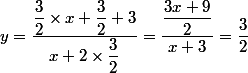
, la droite d'équation horizontale :
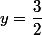
L'ensemble des points pour
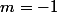
est :
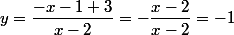
, la droite d'équation horizontale :
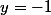
.
3°)
=0\Leftrightarrow xy-3+m(2y-x-1)=0)
Les coordonnées des deux points, indépendantes de

, sont les solutions de ce système :
(y+1) & = & 0\\<br /> x & = & 2y-1<br /> \end{array}<br />\right.<br />\right.)
On en déduit deux couples de solutions :
=\Big(2;\dfrac 3 2\Big))
et
=(-3;-1))
.
4°) Les asymptotes à la courbe d'une fonction homographique :
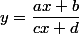
, sont
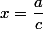
et
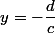
On en déduit les asymptotes à la courbe
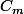
:
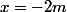
et
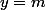
, qui sont les coordonnées du point d'intersection

de ces droites.
A la fin, je suis moins sûr de ma réponse concernant

l'ensemble de points associés à la position de

. En effet, pour le déterminer, je fais la somme
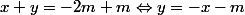
qui est l'équation réduite d'une droite décroissante. Juste ?
Merci d'avance pour vos réponses,
@+ :hein:
